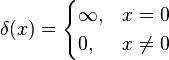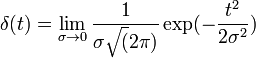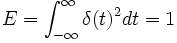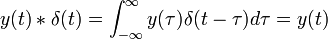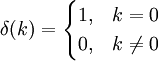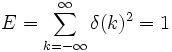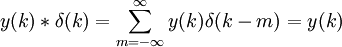Dirac Delta Function

Dirac Function

Definition

The Dirac function 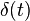$\delta(t)$ is a "signal" with unit energy that is concentrated around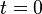 $t = 0$

\delta(x) = \begin{cases} \infty, & x = 0 \\ 0, & x \ne 0 \end{cases}

Alternative definition

\delta(t) = \lim_{\sigma \to 0} \frac{1}{\sigma \sqrt(2\pi)}\exp(-\frac{t^2}{2\sigma^2})

This is a gaussian distribution with spread 0.

Properties

Energy

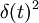E = \int^{\infty}_{-\infty}\delta(t)^2 dt = 1

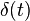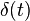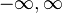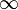NB: $\delta(t)^2$ has no mathematical meaning, as $\delta(t)$ isn't an ordinary function but a distribution. The special nature of $\delta(t)$ appears clearly e.g. when you try to square the same Gaussian distribution above and try to compute the same limit of the integral in $-\infty, \infty$ . The result will be quite surprising: it is $\infty$ !

Convolution

y(t) * \delta(t) = \int^{\infty}_{-\infty} y(\tau)\delta(t - \tau) d\tau = y(t)

Kronecker Delta Function

The Kronecker delta function is the discrete analog of the Dirac function. It has Energy 1 and only a contribution at $k = 0$

\delta(k) = \begin{cases} 1, & k = 0 \\ 0, & k \ne 0 \end{cases}

Properties

Energy

E = \sum^{\infty}_{k = -\infty} \delta(k) ^2 = 1

Convolution

y(k) * \delta(k) = \sum^{\infty}_{m = -\infty} y(k)\delta(k - m) = y(k)

This article is issued from Wikiversity - version of the Wednesday, February 17, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.