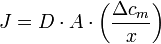Diffusion and osmosis

Diffusion

Educational level: this is a tertiary (university) resource.

Subject classification: this is a science resource .

Resource type: this resource is a lesson.

Simple diffusion is know as the random movement of solute molecules in a solvent tending towards an equilibrium (evenly-distributed) state, a better way to understand this is that diffusion is the net movement of a solute from a region of greater concentration to a region of lower concentration. 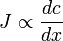The rate of Diffusion (J) is proportional to the conetration gradient over distance x (membrane thickness) $J\propto\frac{dc}{dx}$

Rate of diffusion is independent of diffusion of other substances although is related to

Physical properties of solute and solvent molecules (eg size, electric charge)
temperature
electric field

Diffusion of a solute is rapid over short distances, although the membrane is a selective barrier to diffusion and the concetration gradient lies within the membrane barrier. To truly understand the mechanism of diffusion it must be described quantitavely as Fick's Law of Diffusion

Fick's Law of Diffusion

From a biological perspective Fick's First law 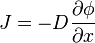$J=-D\frac{\partial\phi}{\partial x}$ gave rise to the Formula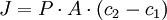 $J={P\cdot A\cdot (c_2 - c_1)}\,\!$

J = the rate of diffusion (mol/sec)
P = the permeability coefficient of solute across membrane (m/sec)
A = membrane area (m²)
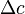
C₂-C₁ = The concentration difference often termed $\Delta c$

J is also related to the diffusion coefficient in the membrane (D),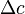 $\Delta c$ within the membrane and the membrane thickness (x) and can be calcualted by means of this equation

J={D\cdot A\cdot \left(\frac {\Delta c_m}{x}\right)}\,\!

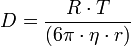
The Diffusion coefficient has various factors contributing to it and can be calcualted using the formula $D=\frac{R\cdot T}{(6\pi \cdot \eta \cdot r)}$

R = Gas constant (8.3 J/K.mol)
T = Absolute temperature (K)
η = Viscosity of barrier
r = Radius of diffusing molecule

The hydrophobic lattice structure of the bilayer acts like a viscous molecular "seive" , also values for P and D are specific for membrane AND diffusing molecules. The solute concentration within a membrane depends on K_p. K_p is the lipid-water coefficient and is described as

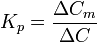K_p=\frac {\Delta C_m}{\Delta C}

For a hydrophobic molecule K_p < 1 and for a hydroophilic molecule K_p < 1, permeability can then be calculated including K_p in the equation and thus gives us 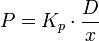$P=K_p\cdot\frac{D}{x}$

Important factors for predicting passive permeability

frictional effects

Molecular size - Small,P↑ ; large . P↓
Molecular shapre - Straight, P↑ ; globular P↓
Membrane Viscostiy - Short R chains, -C=C-, T^ο

Lipid solubility (K_p)

K_p high such as O₂, CO₂, anaesthetics, lipophilic group then P↑
K_p low such as sugars, amino acids, ions , polar/charged groups then P↓

==Osmosis==yeahayeha Osmosis is the net solvent flow, water moves from regions of higher to lower (more negative) water potenials, showing bulk flow. In animals water potential = Osmostive potential (zero for pure water; incresingly negative as solute concentration increases)

Osmolarity is proportional to the concentration of dissolved solutes and inversely proportional to osmotic potential.A common example to describe osmolarity is red blood cells in different salt concetrations if a solution contains a higher concentration of salt than the cells ICF water flows out of the cells and the cell shrinks, this solution is known as Hyperosmotic. Solutions that are at equilibrium with the cell salt concentration are known Isosmotic. If cells are placed in distil water the salt concetration will be larger inside the cell and water will flow into the cell causing it to burst this type of solution is know as Hypoosmotic.

Diffusion and Osmosis Quiz

This article is issued from Wikiversity - version of the Saturday, November 06, 2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.