Damped oscillation

An oscillator is anything that has a rhythmic periodic response. A damped oscillation means an oscillation a oscillation that fades away with time.Examples include a swinging pendulum, a weight on a spring, and also a resistor - inductor - capacitor (RLC) circuit.

Suppose we have an RLC circuit, which has a resistor + inductor + capacitor in series.When the switch closes at time t=0 the capacitor will discharge into a series resistor and inductor.

Now, the voltages and current in this circuit can be given by

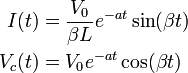
$\begin{align}I(t)&=\frac{V_0}{\beta L}e^{-at}\sin(\beta t)\\ V_c(t)&=V_0 e^{-at}\cos(\beta t)\end{align}$

where

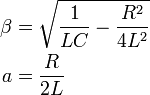
$\begin{align}\beta&=\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}\\ a&=\frac{R}{2L}\end{align}$

and V= initial voltage C = capacitance (farads) R = resistance (ohms) L = inductance (henrys) e = base of natural log (2.71828...)

The above equation is the current for a damped sine wave. It represents a sine wave of maximum amplitude (V/BL) multiplied by a damping factor of an exponential decay. The resulting time variation is an oscillation bounded by a decaying envelope. Critical Damping

We can use these equations to discover when the energy fades out smoothly (over-damped) or rings (under-damped).

Look at the term under the square root sign, which can be simplified to: R²C²-4LC

When R²C²-4LC is positive, then α and β are real numbers and the

oscillator is over-damped. The circuit does not show oscillation

Over damped graph

   * When R²C²-4LC is negative, then α and β are imaginary numbers and the oscillations are
under-damped. The circuit responds with a sine wave in an exponential decay envelope.

Under damped graph

   * When R²C²-4LC is zero, then α and β are zero and oscillations are critically damped.

The circuit response shows a narrow peak followed by an exponential decay.

Critically damped graph

This article is issued from Wikiversity - version of the Thursday, October 20, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.