Coordinate transformations
Vector Transformation in Two Dimensions
In three dimensions, the vector transformation rule is written as
where 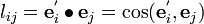 .
.
In two dimensions, this transformation rule is the familiar
In matrix form,
Since we are using sines, the direction of measurement of 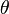 is required. In this case, it is measured counterclockwise.
is required. In this case, it is measured counterclockwise.
Tensor Transformation in Two Dimensions
In three dimensions, the second-order tensor transformation rule is written as
where 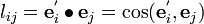 .
.
The Cauchy stress 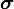 is a symmetric second-order tensor. In two dimensions, the transformation rule for stress is the written as
is a symmetric second-order tensor. In two dimensions, the transformation rule for stress is the written as
In matrix form,
Since we are using sines, the direction of measurement of 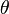 is required. In this case, it is measured counterclockwise.
is required. In this case, it is measured counterclockwise.
Tensor Transformation in two Dimensions, the intrinsic approach
Let construct an orthonormal basis of the second order tensor projected in the first order tensor
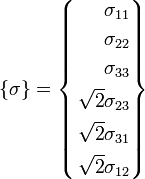
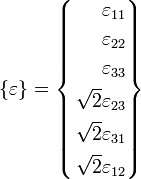
The stress and strain tensors are now defined by :
and
Then once constructs the bound matrix in the orthonormal base 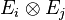
with
![\left [ R(\theta) \right ]](../I/m/551777161507630734bdd6ed724957ad.png) the rotation matrix in
the rotation matrix in 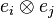 base.
base.
Example
is the rotation along the axis 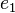 in the :
in the :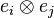 base
base
The associated rotation in the 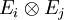 base is :
base is :
The rotation of a second order tensor is now defined by :
Four order tensor
The élasticity tensor 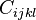 in the :
in the :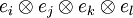 is defined in the :
is defined in the :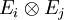 by
by
and is rotated by:
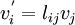
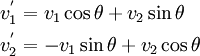
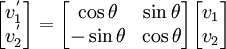
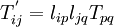
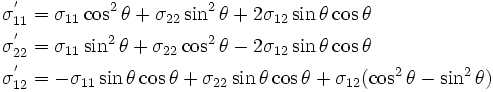
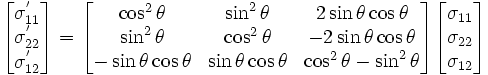
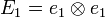
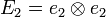
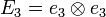
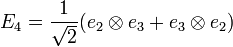
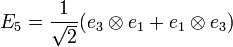
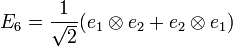
![\left [ \hat{R}(\theta) \right ]=
\left [
\begin{matrix}
R_{11}^2 & R_{12}^2 & R_{13}^2 & \sqrt{2}R_{12}R_{13} & \sqrt{2}R_{11}R_{13} & \sqrt{2}R_{11}R_{12}\\
R_{21}^2 & R_{22}^2 & R_{23}^2 & \sqrt{2}R_{22}R_{23} & \sqrt{2}R_{21}R_{23} & \sqrt{2}R_{22}R_{21}\\
R_{31}^2 & R_{32}^2 & R_{33}^2 & \sqrt{2}R_{33}R_{32} & \sqrt{2}R_{33}R_{31} & \sqrt{2}R_{31}R_{32}\\
\sqrt{2}R_{21}R_{31} & \sqrt{2}R_{22}R_{32} & \sqrt{2}R_{23}R_{33} & R_{22}R_{33}+R_{23}R_{32} & R_{21}R_{33}+R_{31}R_{23} & R_{21}R_{32}+R_{31}R_{22}\\
\sqrt{2}R_{11}R_{31} & \sqrt{2}R_{12}R_{32} & \sqrt{2}R_{13}R_{33} & R_{12}R_{33}+R_{32}R_{13} & R_{11}R_{33}+R_{13}R_{31} & R_{11}R_{32}+R_{31}R_{12}\\
\sqrt{2}R_{11}R_{21} & \sqrt{2}R_{12}R_{22} & \sqrt{2}R_{13}R_{23} & R_{12}R_{23}+R_{22}R_{13} & R_{11}R_{23}+R_{21}R_{13} & R_{11}R_{22}+R_{21}R_{12}\\
\end{matrix} \right ]](../I/m/4f8e99b1c0f0051ce6064a2a65443c5a.png)
![\left [ R(\theta) \right ]=
\left [
\begin{matrix}
1 & 0 & 0 \\
0 & cos \theta & sin \theta \\
0 & -sin \theta& cos \theta
\end{matrix} \right ]](../I/m/106fcaf0dab4bdf7b34c8575afcca4d6.png)
![\left [ \hat{R}(\theta) \right ]=
\left [
\begin{matrix}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & cos^2 \theta & sin^2 \theta & \sqrt{2} sin \theta cos \theta & 0 & 0 \\
0 & sin^2 \theta & cos^2 \theta & -\sqrt{2} sin \theta cos \theta & 0 & 0 \\
0 & - \sqrt{2} sin \theta cos \theta & \sqrt{2} sin \theta cos \theta & cos^2 \theta - sin^2 \theta & 0 & 0\\
0 & 0 & 0 & 0 & cos \theta & -sin \theta \\
0 & 0 & 0 & 0 & sin \theta & cos \theta \\
\end{matrix} \right ]](../I/m/e514b0c5d8440ae227c42cd6a4eb2373.png)
![\left \{ \sigma(\theta) \right \} = {\left [ \hat{R}(\theta) \right ]}^T \left \{ \sigma \right \}](../I/m/9bfc33ae4702a77395dbaf902af957df.png)
![\left [ \overline{C} \right ] = \left[\begin{align}
C_{1111} & C_{1122} & C_{1133} & \sqrt{2}C_{1123} & \sqrt{2}C_{1131} & \sqrt{2}C_{1112} \\
C_{1122} & C_{2222} & C_{2233} & \sqrt{2}C_{2223} & \sqrt{2}C_{2231} & \sqrt{2}C_{2212} \\
C_{1133} & C_{2233} & C_{3333} & \sqrt{2}C_{3323} & \sqrt{2}C_{3331} & \sqrt{2}C_{3312} \\
\sqrt{2}C_{1123} & \sqrt{2}C_{2223} & \sqrt{2}C_{2333} & 2C_{2323} & 2C_{2331} & 2C_{2312} \\
\sqrt{2}C_{1131} & \sqrt{2}C_{2231} & \sqrt{2}C_{3331} & 2C_{2331} & 2C_{3131} & 2C_{3112} \\
\sqrt{2}C_{1112} & \sqrt{2}C_{2212} & \sqrt{2}C_{3312} & 2C_{2312} & 2C_{3112} & 2C_{1212}
\end{align}\right]](../I/m/71744354ca671228bd609e84e3cd333b.png)
![{\left [ \overline{C} (\theta) \right ]}_g = {\left [ \hat{R}(\theta) \right ]}^T \left [ \overline{C} \right ]\left [ \hat{R}(\theta) \right ]](../I/m/609bb5c4e33f82c73d0969b81e4d92f1.png)