Continuum mechanics/Tensor algebra identities
< Continuum mechanicsIdentity 1
Let  and
and 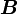 be two second order tensors. Show that
be two second order tensors. Show that
Proof:
Using index notation,
Hence,
Identity 2
Let  be a second order tensor and let
be a second order tensor and let 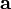 and
and 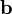 be two
vectors. Show that
be two
vectors. Show that
Proof:
It is convenient to use index notation for this. We have
Hence,
Identity 3
Let  and
and 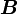 be two second order tensors and let
be two second order tensors and let 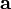 and
and 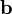 be two vectors. Show that
be two vectors. Show that
Proof:
Using index notation,
Hence,
Identity 4
Let  be a second order tensors and let
be a second order tensors and let 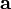 and
and 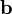 be two vectors. Show that
be two vectors. Show that
Proof:
For the first identity, using index notation, we have
Hence,
For the second identity, we have
Therefore,
Now, ![\mathbf{a}\otimes\mathbf{b} = [\mathbf{b}\otimes\mathbf{a}]^T](../I/m/120dadcd87a4626175c82144b7ee4c25.png) and
and
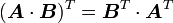 . Hence,
. Hence,
Therefore,
This article is issued from Wikiversity - version of the Tuesday, September 11, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
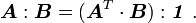
![\boldsymbol{A}:\boldsymbol{B} = A_{ij}~B_{ij} = A^T_{ji}~B_{ij} = A^T_{ji}~B_{ik}~\delta_{jk}
= [\boldsymbol{A}^T\cdot\boldsymbol{B}]_{jk}~\delta_{jk}
= (\boldsymbol{A}^T\cdot\boldsymbol{B}):\boldsymbol{\mathit{1}} ~.](../I/m/4d97ba0f7d255a8ccd552b49f4f4b1dc.png)
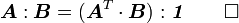
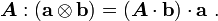
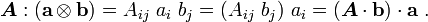
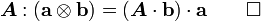
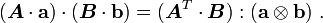
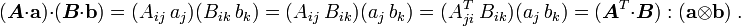
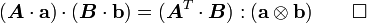
![(\boldsymbol{A}\cdot\mathbf{a})\otimes\mathbf{b} = \boldsymbol{A}\cdot(\mathbf{a}\otimes\mathbf{b})
\qquad
\text{and}
\qquad
\mathbf{a}\otimes(\boldsymbol{A}\cdot\mathbf{b}) = [\boldsymbol{A}\cdot(\mathbf{b}\otimes\mathbf{a})]^T
= (\mathbf{a}\otimes\mathbf{b})\cdot\boldsymbol{A}^T ~.](../I/m/42af3aa8d5db8703941cf2445e52bea6.png)
![[(\boldsymbol{A}\cdot\mathbf{a})\otimes\mathbf{b}]_{ik} = (A_{ij}~a_j)~b_k = A_{ij}~(a_j~b_k)
= A_{ij}~[\mathbf{a}\otimes\mathbf{b}]_{jk}
= \boldsymbol{A}\cdot(\mathbf{a}\otimes\mathbf{b}) ~.](../I/m/ad3f67f2f23bbd2aa1ac4182b5b2355a.png)
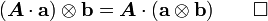
![[\mathbf{a}\otimes(\boldsymbol{A}\cdot\mathbf{b})]_{ij} = a_i~(A_{jk}~b_k)
= (a_i~b_k)~A_{jk} = (a_i~b_k)~A^T_{kj}
= [(\mathbf{a}\otimes\mathbf{b})\cdot\boldsymbol{A}^T]_{ij} ~.](../I/m/d1559c4a9287827f45f88703db16747c.png)
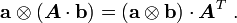
![(\mathbf{a}\otimes\mathbf{b})\cdot\boldsymbol{A}^T = (\mathbf{b}\otimes\mathbf{a})^T\cdot\boldsymbol{A}^T =
[\boldsymbol{A}\cdot(\mathbf{b}\otimes\mathbf{a})]^T ~.](../I/m/6523e45329702b1618783f0ccadb7355.png)
![{
\mathbf{a}\otimes(\boldsymbol{A}\cdot\mathbf{b}) = [\boldsymbol{A}\cdot(\mathbf{b}\otimes\mathbf{a})]^T
= (\mathbf{a}\otimes\mathbf{b})\cdot\boldsymbol{A}^T \qquad \square
}](../I/m/1f823a390c13b3f8e158ce60971855c7.png)