Continuum mechanics/Tensor-vector identities
< Continuum mechanicsTensor-vector identity - 1
Proof:
Using the identity
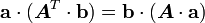 we have
we have
Also, using the definition
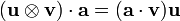 we have
we have
Therefore,
Using the identity
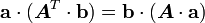 we have
we have
Finally, using the relation
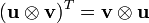 , we get
, we get
Hence,
Tensor-vector identity 2
Let 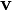 be a vector field and let
be a vector field and let 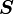 be a second-order tensor field. Let
be a second-order tensor field. Let 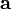 and
and 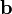 be two arbitrary vectors. Show that
be two arbitrary vectors. Show that
Proof:
Using the identity
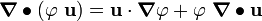 we have
we have
From the identity
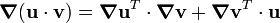 ,
we have
,
we have
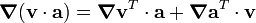 .
.
Since 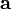 is constant,
is constant, 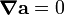 , and we have
, and we have
From the relation
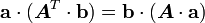 we have
we have
Using the relation 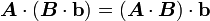 , we
get
, we
get
Therefore, the final form of the first term is
For the second term, from the identity
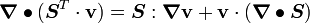 we get,
we get,
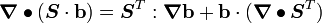 .
.
Since 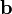 is constant,
is constant, 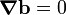 , and we have
, and we have
From the definition
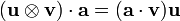 , we get
, we get
Therefore, the final form of the second term is
Adding the two terms, we get
Therefore,
This article is issued from Wikiversity - version of the Tuesday, September 11, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![[(\mathbf{v}\bullet\mathbf{a})(\boldsymbol{S}\bullet\mathbf{b})]\cdot\mathbf{n} =
\mathbf{a}\cdot[\{\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})\}\cdot\mathbf{b}] ~.](../I/m/92fdd2ed050580a01377a200425f67e3.png)
![\mathbf{n}\cdot[(\mathbf{v}\bullet\mathbf{a})(\boldsymbol{S}\bullet\mathbf{b})] =
\mathbf{b}\cdot[(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}^T\cdot\mathbf{n})] ~.](../I/m/2aabfbc8938dc938c7cf12ee27117208.png)
![(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}^T\cdot\mathbf{n}) = [(\boldsymbol{S}^T\cdot\mathbf{n})\otimes\mathbf{v}]\cdot\mathbf{a}~.](../I/m/ff84998492dd1e5d54001cc9bdc28f46.png)
![\mathbf{n}\cdot[(\mathbf{v}\bullet\mathbf{a})(\boldsymbol{S}\bullet\mathbf{b})] =
\mathbf{b}\cdot[\{(\boldsymbol{S}^T\cdot\mathbf{n})\otimes\mathbf{v}\}\cdot\mathbf{a}]~.](../I/m/2378a0aaf6be5cedd90c610858c18255.png)
![\mathbf{b}\cdot[\{(\boldsymbol{S}^T\cdot\mathbf{n})\otimes\mathbf{v}\}\cdot\mathbf{a}] =
\mathbf{a}\cdot[\{(\boldsymbol{S}^T\cdot\mathbf{n})\otimes\mathbf{v}\}^T\cdot\mathbf{b}]~.](../I/m/2608eccd72252b9cc3ab77cbb944e7e7.png)
![\mathbf{a}\cdot[\{(\boldsymbol{S}^T\cdot\mathbf{n})\otimes\mathbf{v}\}^T\cdot\mathbf{b}] =
\mathbf{a}\cdot[\{\mathbf{v}\otimes(\boldsymbol{S}^T\cdot\mathbf{n})\}\cdot\mathbf{b}]~.](../I/m/ece22eec028cc8aca5a26420cdf7ee9a.png)
![{
[(\mathbf{v}\bullet\mathbf{a})(\boldsymbol{S}\bullet\mathbf{b})]\cdot\mathbf{n} =
\mathbf{a}\cdot[\{\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})\}\cdot\mathbf{b}]}
\qquad \qquad \qquad \square](../I/m/ff671d6f664c04a90b1af754f88d11c9.png)
![\boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})] =
\mathbf{a}\cdot[\{\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)\}\cdot\mathbf{b}] ~.](../I/m/2c4d11cdd083e987f5d26f5af55b2597.png)
![\boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})] =
(\boldsymbol{S}\cdot\mathbf{b})\cdot\boldsymbol{\nabla} (\mathbf{v}\cdot\mathbf{a}) +
(\mathbf{v}\cdot\mathbf{a})~\boldsymbol{\nabla} \bullet (\boldsymbol{S}\cdot\mathbf{b}) ~.](../I/m/beeb344dfad9b0309af6bdbcb6072856.png)
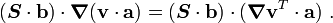
![(\boldsymbol{S}\cdot\mathbf{b})\cdot(\boldsymbol{\nabla} \mathbf{v}^T\cdot\mathbf{a}) =
\mathbf{a}\cdot[\boldsymbol{\nabla} \mathbf{v}\cdot(\boldsymbol{S}\cdot\mathbf{b})] ~.](../I/m/98c1141b305d087a8afbfebe64f1d305.png)
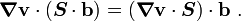
![(\boldsymbol{S}\cdot\mathbf{b})\cdot\boldsymbol{\nabla} (\mathbf{v}\cdot\mathbf{a})=
\mathbf{a}\cdot[(\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S})\cdot\mathbf{b}] ~.](../I/m/c37062b28e4474913c1b82074bcca2f0.png)
![(\mathbf{v}\cdot\mathbf{a})~\boldsymbol{\nabla} \bullet (\boldsymbol{S}\cdot\mathbf{b}) =
(\mathbf{v}\cdot\mathbf{a})~[\mathbf{b}\cdot(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)] =
\mathbf{a}\cdot[\{\mathbf{b}\cdot(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)\}~\mathbf{v}] ~.](../I/m/16921379a89e5d6fe4dfc45ae5499d09.png)
![[\mathbf{b}\cdot(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\mathbf{v} =
[\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]\cdot\mathbf{b} ~.](../I/m/2f8d5d05255f91c49b6869249590f559.png)
![(\mathbf{v}\cdot\mathbf{a})~\boldsymbol{\nabla} \bullet (\boldsymbol{S}\cdot\mathbf{b}) =
\mathbf{a}\cdot[\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]\cdot\mathbf{b} ~.](../I/m/8851a8580ece3d5f21c6210ddc1033dc.png)
![\boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})] =
\mathbf{a}\cdot[(\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S})\cdot\mathbf{b}] +
\mathbf{a}\cdot[\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]\cdot\mathbf{b} ~.](../I/m/8a198d866294266e7b0a9df79bb99c62.png)
![{
\boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})] =
\mathbf{a}\cdot[\{\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)\}\cdot\mathbf{b}] }
\qquad\qquad\qquad\square](../I/m/dc0b26e8962bbc994748cc3a61217f8d.png)