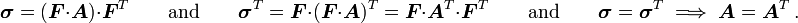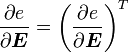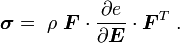Continuum mechanics/Stress-strain relation for thermoelasticity

Relation between Cauchy stress and Green strain

Show that, for thermoelastic materials, the Cauchy stress can be expressed in terms of the Green strain as

\boldsymbol{\sigma} = \rho~\boldsymbol{F}\cdot\frac{\partial e}{\partial \boldsymbol{E}}\cdot\boldsymbol{F}^T ~.

Proof:

Recall that the Cauchy stress is given by

\boldsymbol{\sigma} = \rho~\frac{\partial e}{\partial \boldsymbol{F}}\cdot\boldsymbol{F}^T \qquad \implies \qquad \sigma_{ij} = \rho~\frac{\partial e}{\partial F_{ik}}F^T_{kj} = \rho~\frac{\partial e}{\partial F_{ik}}F_{jk} ~.

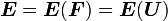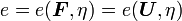The Green strain $\boldsymbol{E} = \boldsymbol{E}(\boldsymbol{F}) = \boldsymbol{E}(\boldsymbol{U})$ and $e = e(\boldsymbol{F},\eta) = e(\boldsymbol{U},\eta)$ . Hence, using the chain rule,

\frac{\partial e}{\partial \boldsymbol{F}} = \frac{\partial e}{\partial \boldsymbol{E}}:\frac{\partial \boldsymbol{E}}{\partial \boldsymbol{F}} \qquad \implies \qquad \frac{\partial e}{\partial F_{ik}} = \frac{\partial e}{\partial E_{lm}}~\frac{\partial E_{lm}}{\partial F_{ik}} ~.

Now,

\boldsymbol{E} = \frac{1}{2}(\boldsymbol{F}^T\cdot\boldsymbol{F} - \boldsymbol{\mathit{1}}) \qquad \implies \qquad E_{lm} = \frac{1}{2}(F^T_{lp}~F_{pm} - \delta_{lm}) = \frac{1}{2}(F_{pl}~F_{pm} - \delta_{lm}) ~.

Taking the derivative with respect to 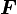$\boldsymbol{F}$ , we get

\frac{\partial \boldsymbol{E}}{\partial \boldsymbol{F}} = \frac{1}{2}\left(\frac{\partial \boldsymbol{F}^T}{\partial \boldsymbol{F}}\cdot\boldsymbol{F} + \boldsymbol{F}^T\cdot\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{F}}\right) \qquad \implies \qquad \frac{\partial E_{lm}}{\partial F_{ik}} = \frac{1}{2}\left(\frac{\partial F_{pl}}{\partial F_{ik}}~F_{pm} + F_{pl}~\frac{\partial F_{pm}}{\partial F_{ik}}\right) ~.

Therefore,

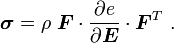
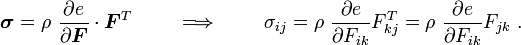
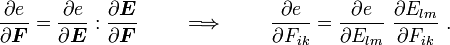
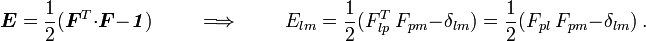
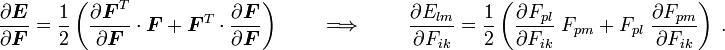
\boldsymbol{\sigma} = \frac{1}{2}~\rho~\left[\frac{\partial e}{\partial \boldsymbol{E}}: \left(\frac{\partial \boldsymbol{F}^T}{\partial \boldsymbol{F}}\cdot\boldsymbol{F} + \boldsymbol{F}^T\cdot\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{F}}\right)\right]\cdot\boldsymbol{F}^T \qquad \implies \qquad \sigma_{ij} = \frac{1}{2}~\rho~\left[\frac{\partial e}{\partial E_{lm}} \left(\frac{\partial F_{pl}}{\partial F_{ik}}~F_{pm} + F_{pl}~\frac{\partial F_{pm}}{\partial F_{ik}}\right)\right]~F_{jk} ~.

Recall,

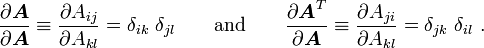
\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} \equiv \frac{\partial A_{ij}}{\partial A_{kl}} = \delta_{ik}~\delta_{jl} \qquad \text{and} \qquad \frac{\partial \boldsymbol{A}^T}{\partial \boldsymbol{A}} \equiv \frac{\partial A_{ji}}{\partial A_{kl}} = \delta_{jk}~\delta_{il} ~.

Therefore,

\sigma_{ij} = \frac{1}{2}~\rho~\left[\frac{\partial e}{\partial E_{lm}} \left(\delta_{pi}~\delta_{lk}~F_{pm} + F_{pl}~\delta_{pi}~\delta_{mk}\right)\right]~F_{jk} = \frac{1}{2}~\rho~\left[\frac{\partial e}{\partial E_{lm}} \left(\delta_{lk}~F_{im} + F_{il}~\delta_{mk}\right)\right]~F_{jk}

or,

\sigma_{ij} = \frac{1}{2}~\rho~\left[\frac{\partial e}{\partial E_{km}}~F_{im} + \frac{\partial e}{\partial E_{lk}}~F_{il}\right]~F_{jk} \qquad \implies \qquad \boldsymbol{\sigma} = \frac{1}{2}~\rho~\left[\boldsymbol{F}\cdot\left(\frac{\partial e}{\partial \boldsymbol{E}}\right)^T + \boldsymbol{F}\cdot\frac{\partial e}{\partial \boldsymbol{E}}\right]\cdot\boldsymbol{F}^T

or,

\boldsymbol{\sigma} = \frac{1}{2}~\rho~\boldsymbol{F}\cdot\left[\left(\frac{\partial e}{\partial \boldsymbol{E}}\right)^T + \frac{\partial e}{\partial \boldsymbol{E}}\right]\cdot\boldsymbol{F}^T ~.

From the symmetry of the Cauchy stress, we have

\boldsymbol{\sigma} = (\boldsymbol{F}\cdot\boldsymbol{A})\cdot\boldsymbol{F}^T \qquad \text{and} \qquad \boldsymbol{\sigma}^T = \boldsymbol{F}\cdot(\boldsymbol{F}\cdot\boldsymbol{A})^T = \boldsymbol{F}\cdot\boldsymbol{A}^T\cdot\boldsymbol{F}^T \qquad \text{and} \qquad \boldsymbol{\sigma} = \boldsymbol{\sigma}^T \implies \boldsymbol{A} = \boldsymbol{A}^T ~.

Therefore,

\frac{\partial e}{\partial \boldsymbol{E}} = \left(\frac{\partial e}{\partial \boldsymbol{E}}\right)^T

and we get

{ \boldsymbol{\sigma} = ~\rho~\boldsymbol{F}\cdot\frac{\partial e}{\partial \boldsymbol{E}}\cdot\boldsymbol{F}^T ~. }

This article is issued from Wikiversity - version of the Tuesday, September 11, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.