Continuum mechanics/Specific heats of thermoelastic materials
< Continuum mechanics|
For thermoelastic materials, show that the specific heats are related by the relation |
Proof:
Recall that
and
Therefore,
Also recall that
Therefore, keeping 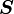 constant while differentiating, we have
constant while differentiating, we have
Noting that 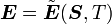 , and
plugging back into the equation for the difference between the two
specific heats, we have
, and
plugging back into the equation for the difference between the two
specific heats, we have
Recalling that
we get
|
For thermoelastic materials, show that the specific heats can also be related by the equations We can also write the above as where |
Proof:
Recall that
Recall the chain rule which states that if
then, if we keep 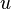 fixed, the partial derivative of
fixed, the partial derivative of 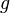 with respect
to
with respect
to 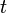 is given by
is given by
In our case,
Hence, we have
Taking the derivative with respect to 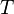 keeping
keeping 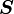 constant, we have
constant, we have
or,
Now,
Therefore,
Again recall that,
Plugging into the above, we get
Therefore, we get the following relation for 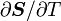 :
:
Recall that
Plugging in the expressions for 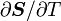 we get:
we get:
Therefore,
Using the identity 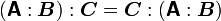 , we have
, we have
|
Consider an isotropic thermoelastic material that has a constant coefficient of thermal expansion and which follows the Saint-Venant–Kirchhoff model, i.e, where Show that the specific heats related by the equation |
Proof:
Recall that,
Plugging the expressions of 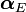 and
and 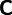 into the above
equation, we have
into the above
equation, we have
Therefore,
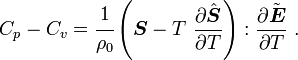
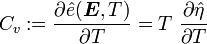
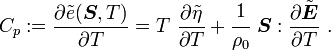
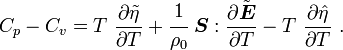
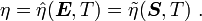
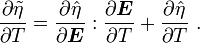
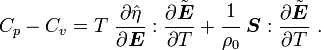
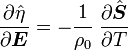
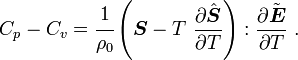
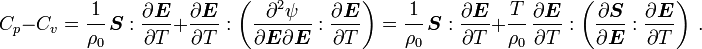
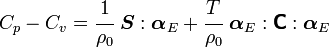
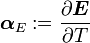 is the thermal expansion tensor and
is the thermal expansion tensor and 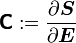 is the stiffness tensor.
is the stiffness tensor.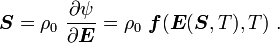
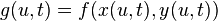
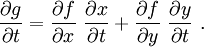
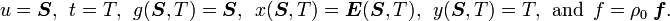
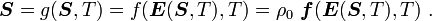
![\frac{\partial g}{\partial T} = \frac{\partial \boldsymbol{S}}{\partial T} =
\rho_0~\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{E}}:
\frac{\partial \boldsymbol{E}}{\partial T} +\frac{\partial \boldsymbol{f}}{\partial T}~\frac{\partial T}{\partial T}\right]](../I/m/e0208a0c423c1633b7402ec1e8f7cb72.png)
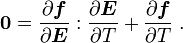
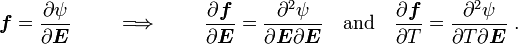
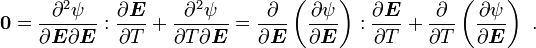
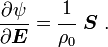
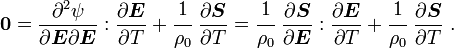
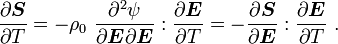
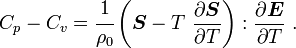
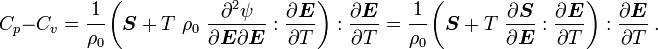
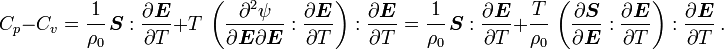
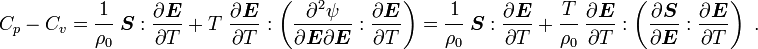

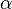 is the coefficient of thermal expansion and
is the coefficient of thermal expansion and 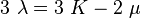 where
where 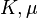 are the bulk and shear moduli, respectively.
are the bulk and shear moduli, respectively. ![C_p - C_v = \cfrac{1}{\rho_0}\left[\alpha~\text{tr}{\boldsymbol{S}} +
9~\alpha^2~K~T\right]~.](../I/m/93df445060a8f71c313ad1165d48c97e.png)
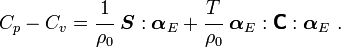
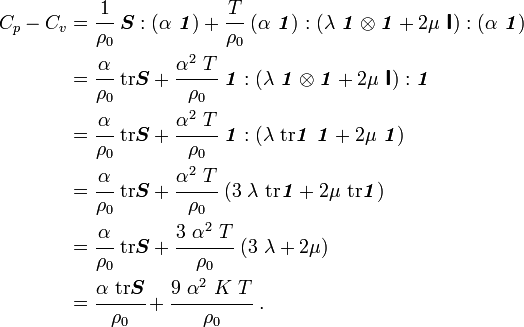
![{
C_p - C_v = \cfrac{1}{\rho_0}\left[\alpha~\text{tr}{\boldsymbol{S}} +
9~\alpha^2~K~T\right]~.
}](../I/m/15771782f5a0ebcb9ed586b1741fe7e0.png)