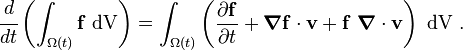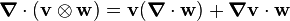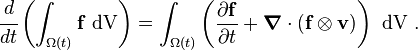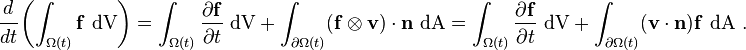Continuum mechanics/Reynolds transport theorem
< Continuum mechanics|
Let This relation is also known as the Reynold's Transport Theorem and is a generalization of the Leibniz rule. Content of example. |
Proof:
Let 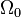 be reference configuration of the region
be reference configuration of the region 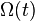 . Let
the motion and the deformation gradient be given by
. Let
the motion and the deformation gradient be given by
Let ![J(\mathbf{X},t) = \det[\boldsymbol{F}(\mathbf{X},t)]](../I/m/7ccc9986952f35bda8ff1f9c49ebf6bf.png) .
Then, integrals in the current and the reference configurations are
related by
.
Then, integrals in the current and the reference configurations are
related by
The time derivative of an integral over a volume is defined as
Converting into integrals over the reference configuration, we get
Since 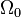 is independent of time, we have
is independent of time, we have
Now, the time derivative of 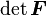 is given by
(see Gurtin: 1981, p. 77)
is given by
(see Gurtin: 1981, p. 77)
Therefore,
where 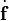 is the material time derivative of
is the material time derivative of 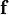 . Now,
the material derivative is given by
. Now,
the material derivative is given by
Therefore,
or,
Using the identity
we then have
Using the divergence theorem and the identity
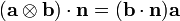 we have
we have
References
- M.E. Gurtin. An Introduction to Continuum Mechanics. Academic Press, New York, 1981.
- T. Belytschko, W. K. Liu, and B. Moran. Nonlinear Finite Elements for Continua and Structures. John Wiley and Sons, Ltd., New York, 2000.
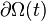 . Let
. Let 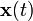 be the positions of points in the region
and let
be the positions of points in the region
and let 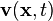 be the velocity field in the region.
Let
be the velocity field in the region.
Let 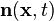 be the
be the 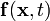 be a vector field in the region
(it may also be a scalar field). Show that
be a vector field in the region
(it may also be a scalar field). Show that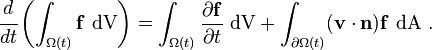
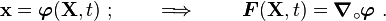
![\int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV} =
\int_{\Omega_0} \mathbf{f}[\boldsymbol{\varphi}(\mathbf{X},t),t]~J(\mathbf{X},t)~\text{dV}_0 =
\int_{\Omega_0} \hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)~\text{dV}_0 ~.](../I/m/6b7ed02827498b2dbe7342fcb16aa68a.png)
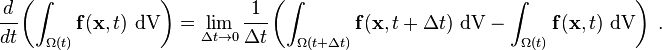
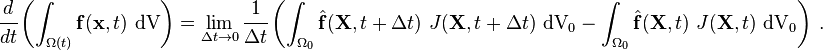
![\begin{align}
\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) & =
\int_{\Omega_0} \left[\lim_{\Delta t \rightarrow 0} \cfrac{
\hat{\mathbf{f}}(\mathbf{X},t+\Delta t)~J(\mathbf{X},t+\Delta t) -
\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)}{\Delta t} \right]~\text{dV}_0 \\
& = \int_{\Omega_0} \frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)]~\text{dV}_0 \\
& = \int_{\Omega_0} \left(
\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]~J(\mathbf{X},t)+
\hat{\mathbf{f}}(\mathbf{X},t)~\frac{\partial }{\partial t}[J(\mathbf{X},t)]\right) ~\text{dV}_0
\end{align}](../I/m/3bde5047de442befcd9dc185f08c26f0.png)
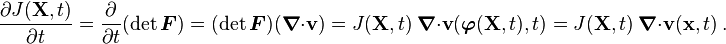
![\begin{align}
\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) & =
\int_{\Omega_0} \left(
\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]~J(\mathbf{X},t)+
\hat{\mathbf{f}}(\mathbf{X},t)~J(\mathbf{X},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right) ~\text{dV}_0 \\
& =
\int_{\Omega_0}
\left(\frac{\partial }{\partial t}[\hat{\mathbf{f}}(\mathbf{X},t)]+
\hat{\mathbf{f}}(\mathbf{X},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~J(\mathbf{X},t) ~\text{dV}_0 \\
& =
\int_{\Omega(t)}
\left(\dot{\mathbf{f}}(\mathbf{x},t)+
\mathbf{f}(\mathbf{x},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~\text{dV}
\end{align}](../I/m/009c6417d46e0f9ef1ebb8426e04fb2a.png)
![\dot{\mathbf{f}}(\mathbf{x},t) =
\frac{\partial \mathbf{f}(\mathbf{x},t)}{\partial t} + [\boldsymbol{\nabla} \mathbf{f}(\mathbf{x},t)]\cdot\mathbf{v}(\mathbf{x},t) ~.](../I/m/5c05c282a558a9ce7dd4f17ec271c626.png)
![\cfrac{d}{dt}\left( \int_{\Omega(t)} \mathbf{f}(\mathbf{x},t)~\text{dV}\right) =
\int_{\Omega(t)}
\left(
\frac{\partial \mathbf{f}(\mathbf{x},t)}{\partial t} + [\boldsymbol{\nabla} \mathbf{f}(\mathbf{x},t)]\cdot\mathbf{v}(\mathbf{x},t) +
\mathbf{f}(\mathbf{x},t)~\boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{x},t)\right)~\text{dV}](../I/m/f1a4f88166e8f0c07a1bc8d93affef7b.png)