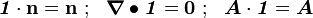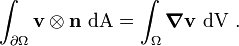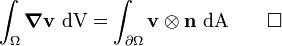Continuum mechanics/Relations between surface and volume integrals
< Continuum mechanicsSurface-volume integral relation 1
Let  be a body and let
be a body and let  be its surface. Let
be its surface. Let 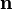 be
the normal to the surface. Let
be
the normal to the surface. Let 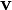 be a vector field on
be a vector field on  and let
and let 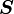 be a second-order tensor field on
be a second-order tensor field on  . Show that
. Show that
Proof:
Recall the relation
Integrating over the volume, we have
Since 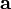 and
and 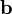 are constant, we have
are constant, we have
From the divergence theorem,
we get
Using the relation
we get
Since 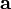 and
and 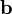 are constant, we have
are constant, we have
Therefore,
Since 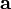 and
and 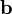 are arbitrary, we have
are arbitrary, we have
Surface-volume integral relation 2
Let  be a body and let
be a body and let 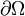 be its surface. Let
be its surface. Let 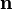 be
the normal to the surface. Let
be
the normal to the surface. Let 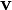 be a vector field on
be a vector field on  .
Show that
.
Show that
Proof:
Recall that
where 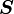 is any second-order tensor field on
is any second-order tensor field on  . Let us assume
that
. Let us assume
that 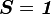 . Then we have
. Then we have
Now,
where  is any second-order tensor. Therefore,
is any second-order tensor. Therefore,
Rearranging,
This article is issued from Wikiversity - version of the Tuesday, September 11, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![\int_{\partial{\Omega}} \mathbf{v}\otimes(\boldsymbol{S}^T\cdot\mathbf{n})~\text{dA} =
\int_{\Omega} [\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\text{dV} ~.](../I/m/78bfe2165fe145e51793b421694ad530.png)
![\boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})] =
\mathbf{a}\cdot[\{\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)\}\cdot\mathbf{b}] ~.](../I/m/2c4d11cdd083e987f5d26f5af55b2597.png)
![\int_{\Omega} \boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]~\text{dV} =
\int_{\Omega}
\mathbf{a}\cdot[\{\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} +
\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)\}\cdot\mathbf{b}~\text{dV}~.](../I/m/4228b5504e6f3be5b1fccef8f3328f73.png)
![\int_{\Omega} \boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]~\text{dV} =
\mathbf{a}\cdot\left[\left\{\int_{\Omega}
[\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} +
\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\text{dV}\right\}\cdot\mathbf{b}\right]~.](../I/m/917847585060be153ac7f8ea2494e2e0.png)
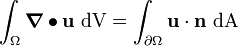
![\int_{\Omega} \boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]~\text{dV} =
\int_{\partial{\Omega}} [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]\cdot\mathbf{n}~\text{dA} ~.](../I/m/b0a6d64b806af6ac9b6723a666a3ddb6.png)
![[(\mathbf{v}\bullet\mathbf{a})(\boldsymbol{S}\bullet\mathbf{b})]\cdot\mathbf{n} =
\mathbf{a}\cdot[\{\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})\}\cdot\mathbf{b}]](../I/m/3548786d7e3e22bd0886045fc48b578c.png)
![\int_{\Omega} \boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]~\text{dV} =
\int_{\partial{\Omega}}
\mathbf{a}\cdot[\{\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})\}\cdot\mathbf{b}]~\text{dA} ~.](../I/m/8a1d120d4bccc2bdff1b5ce73365d577.png)
![\int_{\Omega} \boldsymbol{\nabla} \bullet [(\mathbf{v}\cdot\mathbf{a})(\boldsymbol{S}\cdot\mathbf{b})]~\text{dV} =
\mathbf{a}\cdot\left[\left\{\int_{\partial{\Omega}}
\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})~\text{dA}\right\}\cdot\mathbf{b}\right] ~.](../I/m/293d07ae6e7afe30eacf300a2cc80343.png)
![\mathbf{a}\cdot\left[\left\{\int_{\partial{\Omega}}
\mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})~\text{dA}\right\}\cdot\mathbf{b}\right]=
\mathbf{a}\cdot\left[\left\{\int_{\Omega}
[\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} +
\mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\text{dV}\right\}\cdot\mathbf{b}\right]~.](../I/m/23daad114506bd5c7d3c308f5d33bd25.png)
![{
\int_{\partial{\Omega}} \mathbf{v}\otimes(\boldsymbol{S}^T\bullet\mathbf{n})~\text{dA} =
\int_{\Omega} [\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\text{dV} }
\qquad\qquad\qquad\square](../I/m/e962009cc11134e14562457beb85c2ae.png)
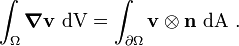
![\int_{\partial{\Omega}} \mathbf{v}\otimes(\boldsymbol{S}^T\cdot\mathbf{n})~\text{dA} =
\int_{\Omega} [\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{S} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{S}^T)]~\text{dV}](../I/m/d47debe3ed9d86e43bfde2e1108bbb49.png)
![\int_{\partial{\Omega}} \mathbf{v}\otimes(\boldsymbol{\mathit{1}}\cdot\mathbf{n})~\text{dA} =
\int_{\Omega} [\boldsymbol{\nabla} \mathbf{v}\cdot\boldsymbol{\mathit{1}} + \mathbf{v}\otimes(\boldsymbol{\nabla} \bullet \boldsymbol{\mathit{1}})]~\text{dV}](../I/m/796b962ea6984d91dc70941df91920fe.png)