Continuum mechanics/Motion and displacement
< Continuum mechanicsContinuum Mechanics
To understand the updated Lagrangian formulation and nonlinear finite elements of solids, we have to know continuum mechanics. A brief introduction to continuum mechanics is given in the following. If you find this handout difficult to follow, please read Chapter 2 from Belytschko's book and Chapter 9 from Reddy's book. You should also read an introductory text on continuum mechanics such as Nonlinear continuum mechanics for finite element analysis by Bonet and Wood.
Motion
Let the undeformed (or reference) configuration of the body be 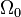 and let the undeformed boundary be
and let the undeformed boundary be 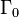 . Let the deformed (or current) configuration be
. Let the deformed (or current) configuration be 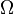 with boundary
with boundary 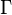 . Let
. Let 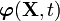 be the motion that takes the body from the reference to the current configuration (see Figure 1).
be the motion that takes the body from the reference to the current configuration (see Figure 1).
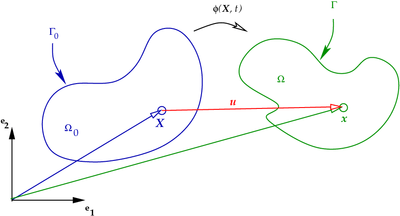 Figure 1. The motion of a body. |
We write
where 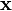 is the position of material point
is the position of material point 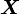 at time
at time 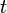 .
.
In index notation,
Displacement
The displacement of a material point is given by
In index notation,
where 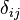 is the Kronecker delta.
is the Kronecker delta.
Velocity
The velocity is the material time derivative of the motion (i.e., the time derivative with 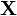 held constant). This type of derivative is also called the total derivative.
held constant). This type of derivative is also called the total derivative.
Now,
Therefore, the material time derivative of 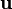 is
is
Alternatively, we could have expressed the velocity in terms of the
spatial coordinates 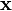 . Let
. Let
Then the material time derivative of 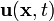 is
is
Acceleration
The acceleration is the material time derivative of the velocity of a material point.
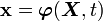
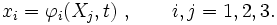
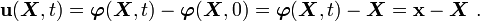
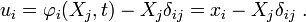
![\mathbf{v}(\boldsymbol{X}, t) = \frac{\partial }{\partial t}\left[\boldsymbol{\varphi}(\boldsymbol{X}, t)\right] ~.](../I/m/7dd26d549fb197dc981dec320cdce6f6.png)
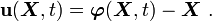
![\dot{\mathbf{u}} = \frac{\partial }{\partial t}\left[\mathbf{u}(\boldsymbol{X},t)\right] =
\frac{\partial }{\partial t}\left[\boldsymbol{\varphi}(\boldsymbol{X},t) - \boldsymbol{X}\right] =
\frac{\partial }{\partial t}\left[\boldsymbol{\varphi}(\boldsymbol{X},t)\right] = \mathbf{v}(\boldsymbol{X}, t) ~.](../I/m/e24d09e225f2002c95c5356823bbab13.png)
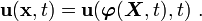
![\cfrac{D}{Dt}\left[\mathbf{u}(\mathbf{x}, t)\right] =
\frac{\partial \mathbf{u}}{\partial t} + \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\frac{\partial \mathbf{x}}{\partial t} =
\frac{\partial \mathbf{u}}{\partial t} + \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\frac{\partial }{\partial t}
\left[\boldsymbol{\varphi}(\boldsymbol{X},t)\right] =
\mathbf{v}(\mathbf{x},t) + \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\mathbf{v}(\boldsymbol{X},t) ~.](../I/m/914aa1fde45e74b93f6df8ee3c28e66c.png)
![\mathbf{a}(\boldsymbol{X}, t) = \frac{\partial }{\partial t}\left[\mathbf{v}(\boldsymbol{X}, t)\right] = \dot{\mathbf{v}}
= \frac{\partial^2 }{\partial t^2}\left[\mathbf{u}(\boldsymbol{X},t)\right] = \ddot{\mathbf{u}} ~.](../I/m/14a73bbba31352e5e7576604fee4b7a7.png)