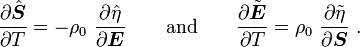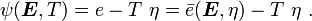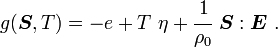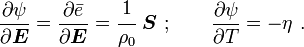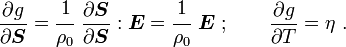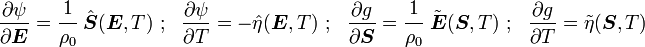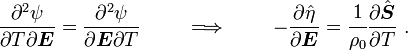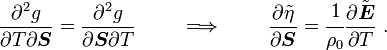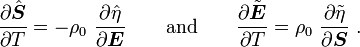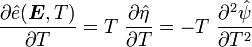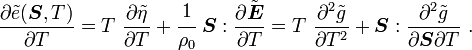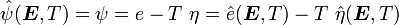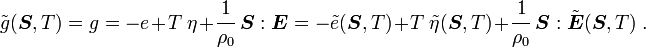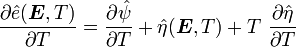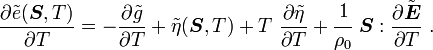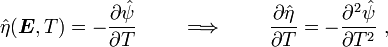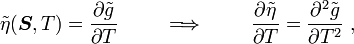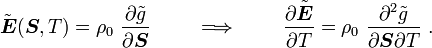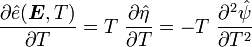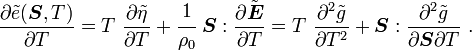Continuum mechanics/Maxwell relations for thermoelasticity
< Continuum mechanics|
For thermoelastic materials, show that the following relations hold: where Also show that |
Proof:
Recall that
and
(Note that we can choose any functional dependence that we like, because
the quantities  ,
, 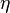 ,
, 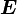 are the actual quantities and not any
particular functional relations).
are the actual quantities and not any
particular functional relations).
The derivatives are
and
Hence,
From the above, we have
and
Hence,
|
For thermoelastic materials, show that the following relations hold: and |
Proof:
Recall,
and
Therefore,
and
Also, recall that
and
Hence,
and
This article is issued from Wikiversity - version of the Tuesday, September 11, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
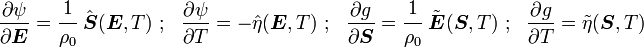
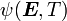 is the Helmholtz free energy and
is the Helmholtz free energy and 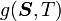 is the Gibbs free energy.
is the Gibbs free energy.