Continuum mechanics/Leibniz formula
< Continuum mechanics|
The integral is a function of the parameter This relation is also known as the Leibniz rule. |
Proof:
We have,
Now,
Since 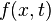 is essentially constant over the infinitesimal
intervals
is essentially constant over the infinitesimal
intervals 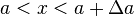 and
and 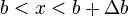 , we may write
, we may write
Taking the limit as 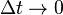 , we get
, we get
or,
This article is issued from Wikiversity - version of the Sunday, February 01, 2009. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
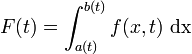
 . Show that the derivative of
. Show that the derivative of 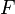 is given by
is given by![\cfrac{dF}{dt} = \cfrac{d}{dt}\left( \int_{a(t)}^{b(t)} f(x, t)~\text{dx}
\right) = \int_{a(t)}^{b(t)} \frac{\partial f(x, t)}{\partial t}~\text{dx} +
f[b(t),t]~\frac{\partial b(t)}{\partial t} - f[a(t),t]~\frac{\partial a(t)}{\partial t}~.](../I/m/18ed811921927f4aaef5544827a5b00d.png)
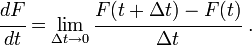
![\begin{align}
\cfrac{F(t + \Delta t) - F(t)}{\Delta t} & =
\cfrac{1}{\Delta t} \left[
\int_{a(t+\Delta t)}^{b(t+\Delta t)} f(x, t+\Delta t)~\text{dx} -
\int_{a(t)}^{b(t)} f(x, t)~\text{dx}\right] \\
& \equiv
\cfrac{1}{\Delta t} \left[
\int_{a+\Delta a}^{b+\Delta b} f(x, t+\Delta t)~\text{dx} -
\int_{a}^{b} f(x, t)~\text{dx}\right] \\
& =
\cfrac{1}{\Delta t} \left[
-\int_{a}^{a+\Delta a} f(x, t+\Delta t)~\text{dx} +
\int_{a}^{b+\Delta b} f(x, t+\Delta t)~\text{dx} -
\int_{a}^{b} f(x, t)~\text{dx}\right] \\
& =
\cfrac{1}{\Delta t} \left[
-\int_{a}^{a+\Delta a} f(x, t+\Delta t)~\text{dx} +
\int_{a}^{b} f(x, t+\Delta t)~\text{dx} +
\int_{b}^{b+\Delta b} f(x, t+\Delta t)~\text{dx} -
\int_{a}^{b} f(x, t)~\text{dx}\right] \\
& =
\int_{a}^{b} \cfrac{f(x, t+\Delta t) - f(x,t)}{\Delta t}~\text{dx} +
\cfrac{1}{\Delta t}\int_{b}^{b+\Delta b} f(x, t+\Delta t)~\text{dx} -
\cfrac{1}{\Delta t}\int_{a}^{a+\Delta a} f(x, t+\Delta t)~\text{dx} ~.
\end{align}](../I/m/dc43d7a1d1d121ad6507e3f6264ec27f.png)
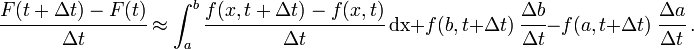
![\lim_{\Delta t \rightarrow 0} \left[\cfrac{F(t + \Delta t) - F(t)}{\Delta t}\right] =
\lim_{\Delta t \rightarrow 0}\left[
\int_{a}^{b} \cfrac{f(x, t+\Delta t) - f(x,t)}{\Delta t}~\text{dx}\right]
+ \lim_{\Delta t \rightarrow 0}\left[f(b, t+\Delta t)~\cfrac{\Delta b}{\Delta t}\right] -
\lim_{\Delta t \rightarrow 0}\left[f(a, t+\Delta t)~\cfrac{\Delta a}{\Delta t}\right]](../I/m/ab4c567e90c69b7414eb9542b78e3272.png)
![{
\cfrac{dF(t)}{dt} =
\int_{a(t)}^{b(t)} \frac{\partial f(x, t)}{\partial t}~\text{dx} +
f[b(t),t]~\frac{\partial b(t)}{\partial t} - f[a(t),t]~\frac{\partial a(t)}{\partial t}~.
} \qquad\qquad\qquad\square](../I/m/f476ba39e19fa74dc8e341e2af9471fb.png)