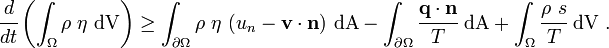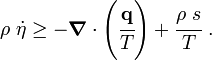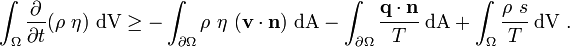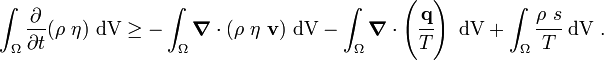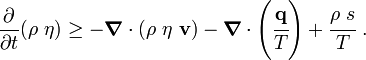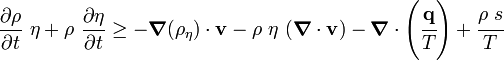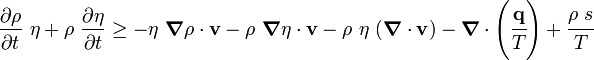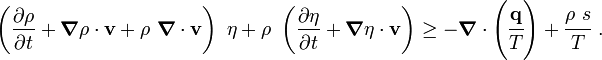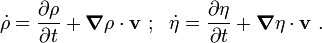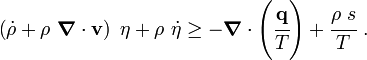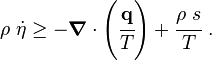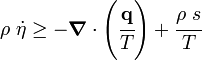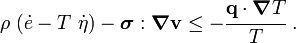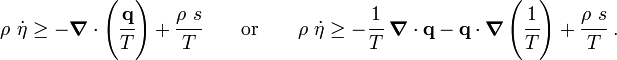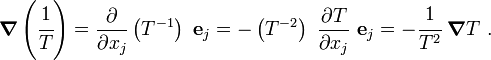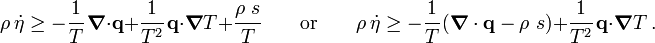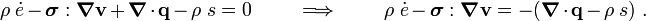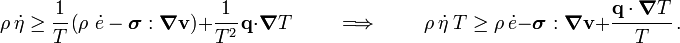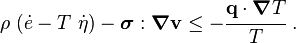Continuum mechanics/Entropy inequality

< Continuum mechanics

The Clausius-Duhem inequality can be expressed in integral form as

\cfrac{d}{dt}\left(\int_{\Omega} \rho~\eta~\text{dV}\right) \ge \int_{\partial \Omega} \rho~\eta~(u_n - \mathbf{v}\cdot\mathbf{n})~\text{dA} - \int_{\partial \Omega} \cfrac{\mathbf{q}\cdot\mathbf{n}}{T}~\text{dA} + \int_{\Omega} \cfrac{\rho~s}{T}~\text{dV} ~.

In differential form the Clusius-Duhem inequality can be written as

\rho~\dot{\eta} \ge - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} ~.

Proof:

Assume that $\Omega$ is an arbitrary fixed control volume. Then $u_n = 0$ and the derivative can be taken inside the integral to give

\int_{\Omega} \frac{\partial }{\partial t}(\rho~\eta)~\text{dV} \ge -\int_{\partial \Omega} \rho~\eta~(\mathbf{v}\cdot\mathbf{n})~\text{dA} - \int_{\partial \Omega} \cfrac{\mathbf{q}\cdot\mathbf{n}}{T}~\text{dA} + \int_{\Omega} \cfrac{\rho~s}{T}~\text{dV} ~.

Using the divergence theorem, we get

\int_{\Omega} \frac{\partial }{\partial t}(\rho~\eta)~\text{dV} \ge -\int_{\Omega} \boldsymbol{\nabla} \cdot (\rho~\eta~\mathbf{v})~\text{dV} - \int_{\Omega} \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right)~\text{dV} + \int_{\Omega} \cfrac{\rho~s}{T}~\text{dV} ~.

Since $\Omega$ is arbitrary, we must have

\frac{\partial }{\partial t}(\rho~\eta) \ge -\boldsymbol{\nabla} \cdot (\rho~\eta~\mathbf{v}) - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} ~.

Expanding out

\frac{\partial \rho}{\partial t}~\eta + \rho~\frac{\partial \eta}{\partial t} \ge -\boldsymbol{\nabla} (\rho_\eta)\cdot\mathbf{v} - \rho~\eta~(\boldsymbol{\nabla} \cdot \mathbf{v}) - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T}

or,

\frac{\partial \rho}{\partial t}~\eta + \rho~\frac{\partial \eta}{\partial t} \ge -\eta~\boldsymbol{\nabla} \rho\cdot\mathbf{v} - \rho~\boldsymbol{\nabla} \eta\cdot\mathbf{v} - \rho~\eta~(\boldsymbol{\nabla} \cdot \mathbf{v}) - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T}

or,

\left(\frac{\partial \rho}{\partial t} + \boldsymbol{\nabla} \rho\cdot\mathbf{v} + \rho~\boldsymbol{\nabla} \cdot \mathbf{v}\right) ~\eta + \rho~\left(\frac{\partial \eta}{\partial t} + \boldsymbol{\nabla} \eta\cdot\mathbf{v}\right) \ge -\boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} ~.

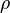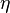Now, the material time derivatives of $\rho$ and $\eta$ are given by

\dot{\rho} = \frac{\partial \rho}{\partial t} + \boldsymbol{\nabla} \rho\cdot\mathbf{v} ~;~~ \dot{\eta} = \frac{\partial \eta}{\partial t} + \boldsymbol{\nabla} \eta\cdot\mathbf{v} ~.

Therefore,

\left(\dot{\rho} + \rho~\boldsymbol{\nabla} \cdot \mathbf{v}\right)~\eta + \rho~\dot{\eta} \ge -\boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} ~.

From the conservation of mass $\dot{\rho} + \rho~\boldsymbol{\nabla} \cdot \mathbf{v} = 0$ . Hence,

{ \rho~\dot{\eta} \ge -\boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} ~. }

In terms of the specific entropy, the Clausius-Duhem inequality is written as

\rho~\dot{\eta} \ge - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T}

Show that the inequality can be expressed in terms of the internal energy as

\rho~(\dot{e} - T~\dot{\eta}) - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~.

Proof:

Using the identity 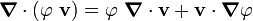$\boldsymbol{\nabla} \cdot (\varphi~\mathbf{v}) = \varphi~\boldsymbol{\nabla} \cdot \mathbf{v} + \mathbf{v}\cdot\boldsymbol{\nabla} \varphi$ in the Clausius-Duhem inequality, we get

\rho~\dot{\eta} \ge - \boldsymbol{\nabla} \cdot \left(\cfrac{\mathbf{q}}{T}\right) + \cfrac{\rho~s}{T} \qquad\text{or}\qquad \rho~\dot{\eta} \ge - \cfrac{1}{T}~\boldsymbol{\nabla} \cdot \mathbf{q} - \mathbf{q}\cdot\boldsymbol{\nabla} \left(\cfrac{1}{T}\right) + \cfrac{\rho~s}{T} ~.

Now, using index notation with respect to a Cartesian basis 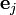$\mathbf{e}_j$ ,

\boldsymbol{\nabla} \left(\cfrac{1}{T}\right) = \frac{\partial }{\partial x_j}\left(T^{-1}\right)~\mathbf{e}_j = -\left(T^{-2}\right)~\frac{\partial T}{\partial x_j}~\mathbf{e}_j = -\cfrac{1}{T^2}~\boldsymbol{\nabla} T ~.

Hence,

\rho~\dot{\eta} \ge - \cfrac{1}{T}~\boldsymbol{\nabla} \cdot \mathbf{q} + \cfrac{1}{T^2}~\mathbf{q}\cdot\boldsymbol{\nabla} T + \cfrac{\rho~s}{T} \qquad\text{or}\qquad \rho~\dot{\eta} \ge -\cfrac{1}{T}\left(\boldsymbol{\nabla} \cdot \mathbf{q} - \rho~s\right) + \cfrac{1}{T^2}~\mathbf{q}\cdot\boldsymbol{\nabla} T ~.

Recall the balance of energy

\rho~\dot{e} - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} + \boldsymbol{\nabla} \cdot \mathbf{q} - \rho~s = 0 \qquad \implies \qquad \rho~\dot{e} - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} = - (\boldsymbol{\nabla} \cdot \mathbf{q} - \rho~s) ~.

Therefore,

\rho~\dot{\eta} \ge \cfrac{1}{T}\left(\rho~\dot{e}-\boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v}\right) + \cfrac{1}{T^2}~\mathbf{q}\cdot\boldsymbol{\nabla} T \qquad \implies \qquad \rho~\dot{\eta}~T \ge \rho~\dot{e}-\boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} + \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~.

Rearranging,

{ \rho~(\dot{e} - T~\dot{\eta}) - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~. }

This article is issued from Wikiversity - version of the Wednesday, September 19, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.