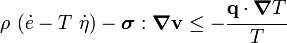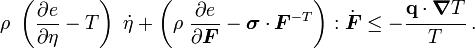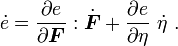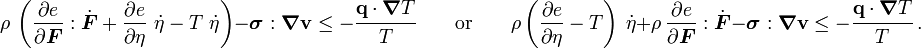Continuum mechanics/Clausius-Duhem inequality for thermoelasticity

Clausius-Duhem inequality for thermoelasticity

For thermoelastic materials, the internal energy is a function only of the deformation gradient and the temperature, i.e., $e = e(\boldsymbol{F}, T)$ . Show that, for thermoelastic materials, the Clausius-Duhem inequality

\rho~(\dot{e} - T~\dot{\eta}) - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T}

can be expressed as

\rho~\left(\frac{\partial e}{\partial \eta} - T\right)~\dot{\eta} + \left(\rho~\frac{\partial e}{\partial \boldsymbol{F}} - \boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T}\right):\dot{\boldsymbol{F}} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~.

Proof:

Since $e = e(\boldsymbol{F}, T)$ , we have

\dot{e} = \frac{\partial e}{\partial \boldsymbol{F}}:\dot{\boldsymbol{F}} + \frac{\partial e}{\partial \eta}~\dot{\eta} ~.

Therefore,

\rho~\left(\frac{\partial e}{\partial \boldsymbol{F}}:\dot{\boldsymbol{F}} + \frac{\partial e}{\partial \eta}~\dot{\eta} - T~\dot{\eta}\right) - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} \qquad\text{or}\qquad \rho\left(\frac{\partial e}{\partial \eta} - T\right)~\dot{\eta} + \rho~\frac{\partial e}{\partial \boldsymbol{F}}:\dot{\boldsymbol{F}} - \boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~.

Now, $\boldsymbol{\nabla}\mathbf{v} = \boldsymbol{l} = \dot{\boldsymbol{F}}\cdot\boldsymbol{F}^{-1}$ . Therefore, using the identity $\boldsymbol{A}:(\boldsymbol{B}\cdot\boldsymbol{C}) = (\boldsymbol{A}\cdot\boldsymbol{C}^T):\boldsymbol{B}$ , we have

\boldsymbol{\sigma}:\boldsymbol{\nabla}\mathbf{v} = \boldsymbol{\sigma}:(\dot{\boldsymbol{F}}\cdot\boldsymbol{F}^{-1}) = (\boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T}):\dot{\boldsymbol{F}} ~.

Hence,

\rho\left(\frac{\partial e}{\partial \eta} - T\right)~\dot{\eta} + \rho~\frac{\partial e}{\partial \boldsymbol{F}}:\dot{\boldsymbol{F}} - (\boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T}):\dot{\boldsymbol{F}} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T}

or,

\rho~\left(\frac{\partial e}{\partial \eta} - T\right)~\dot{\eta} + \left(\rho~\frac{\partial e}{\partial \boldsymbol{F}} - \boldsymbol{\sigma}\cdot\boldsymbol{F}^{-T}\right):\dot{\boldsymbol{F}} \le - \cfrac{\mathbf{q}\cdot\boldsymbol{\nabla} T}{T} ~.

This article is issued from Wikiversity - version of the Wednesday, July 01, 2009. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.