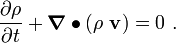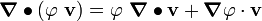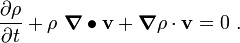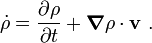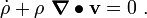Continuum mechanics/Balance of mass
< Continuum mechanicsStatement of the balance of mass
The balance of mass can be expressed as:
where 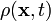 is the current mass density,
is the current mass density, 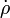 is
the material time derivative of
is
the material time derivative of 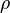 , and
, and 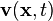 is the
velocity of physical particles in the body
is the
velocity of physical particles in the body  bounded by
the surface
bounded by
the surface 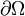 .
.
Proof
We can show how this relation is derived by recalling that the general equation for the balance of a physical quantity
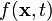 is given by
is given by
To derive the equation for the balance of mass, we assume that the
physical quantity of interest is the mass density 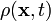 .
Since mass is neither created or destroyed, the surface and interior
sources are zero, i.e.,
.
Since mass is neither created or destroyed, the surface and interior
sources are zero, i.e., 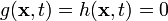 . Therefore, we have
. Therefore, we have
Let us assume that the volume  is a control volume (i.e., it
does not change with time). Then the surface
is a control volume (i.e., it
does not change with time). Then the surface 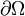 has a zero
velocity (
has a zero
velocity (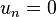 ) and we get
) and we get
Using the divergence theorem
we get
or,
Since  is arbitrary, we must have
is arbitrary, we must have
Using the identity
we have
Now, the material time derivative of 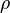 is defined as
is defined as
Therefore,
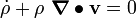
![\cfrac{d}{dt}\left[\int_{\Omega} f(\mathbf{x},t)~\text{dV}\right] =
\int_{\partial{\Omega}} f(\mathbf{x},t)[u_n(\mathbf{x},t) - \mathbf{v}(\mathbf{x},t)\cdot\mathbf{n}(\mathbf{x},t)]~\text{dA} +
\int_{\partial{\Omega}} g(\mathbf{x},t)~\text{dA} + \int_{\Omega} h(\mathbf{x},t)~\text{dV} ~.](../I/m/3c69e1cd86d9e8ff87d1d8359eae78da.png)
![\cfrac{d}{dt}\left[\int_{\Omega} \rho(\mathbf{x},t)~\text{dV}\right] =
\int_{\partial{\Omega}} \rho(\mathbf{x},t)[u_n(\mathbf{x},t) - \mathbf{v}(\mathbf{x},t)\cdot\mathbf{n}(\mathbf{x},t)]~\text{dA}~.](../I/m/02c33cb64d4da9d27ba575ad9962a28f.png)
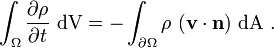
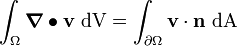
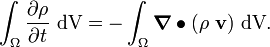
![\int_{\Omega} \left[\frac{\partial \rho}{\partial t} + \boldsymbol{\nabla} \bullet (\rho~\mathbf{v})\right]~\text{dV} = 0 ~.](../I/m/6941f66766f35abdf8aa7dc671598a5b.png)