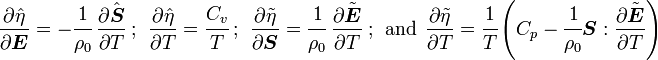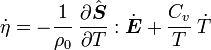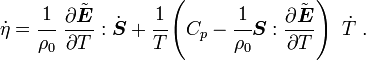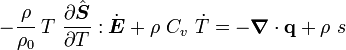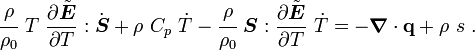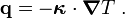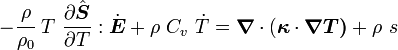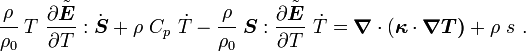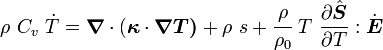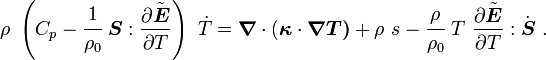Continuum mechanics/Balance of energy for thermoelasticity
< Continuum mechanics|
Show that, for thermoelastic materials, the balance of energy can be expressed as |
Proof:
Since 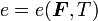 , we have
, we have
Plug into energy equation to get
Recall,
Hence,
Now,  . Therefore, using the
identity
. Therefore, using the
identity 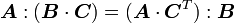 , we have
, we have
Plugging into the energy equation, we have
or,
|
For thermoelastic materials, the specific internal energy is given by where where |
Taking the material time derivative of the specific internal energy, we get
Now, for thermoelastic materials,
Therefore,
Now,
Therefore,
Also,
Hence,
|
For thermoelastic materials, show that the balance of energy equation can be expressed as either or where For the special case where there are no sources and we can ignore heat conduction (for very fast processes), the energy equation simplifies to where |
Proof:
If the independent variables are 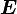 and
and 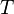 , then
, then
On the other hand, if we consider 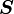 and
and 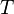 to be the independent
variables
to be the independent
variables
Since
we have, either
or
The equation for balance of energy in terms of the specific entropy is
Using the two forms of 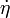 , we get two forms of the energy equation:
, we get two forms of the energy equation:
and
From Fourier's law of heat conduction
Therefore,
and
Rearranging,
or,
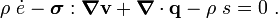

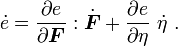
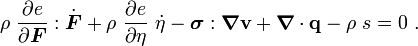
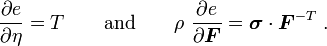
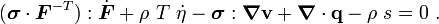
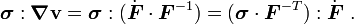
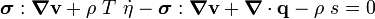

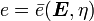
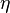 is the specific entropy. Show that
is the specific entropy. Show that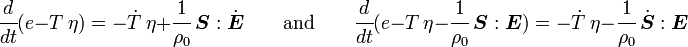
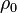 is the initial density,
is the initial density, 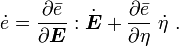
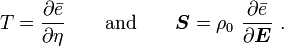
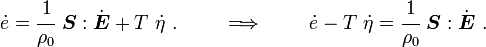
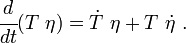
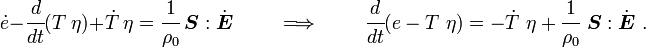
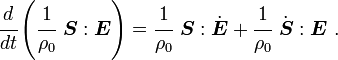
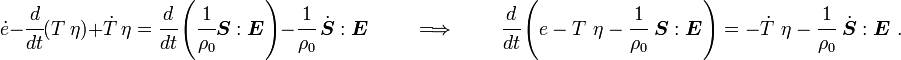
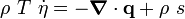
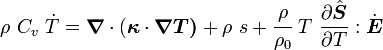
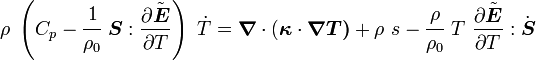
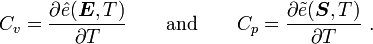
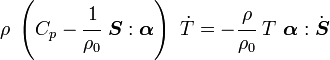
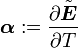 is the thermal expansion tensor which has the form
is the thermal expansion tensor which has the form 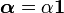 for isotropic materials and
for isotropic materials and 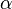 is the coefficient of thermal expansion. The above equation can be used to calculate the change of temperature in thermoelasticity.
is the coefficient of thermal expansion. The above equation can be used to calculate the change of temperature in thermoelasticity.