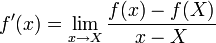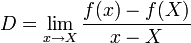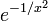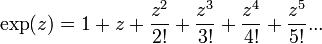Complex analytic function

Mathematics

Analytic function

Subject classification: this is a mathematics resource .

Educational level: this is a secondary education resource.

Educational level: this is a tertiary (university) resource.

A complex function is a function that takes a complex argument and yields a complex result. The simplest examples of such functions are the common real functions that can be defined by a power series. Just use the same power series, while allowing the function argument to be complex.

If a complex function is differentiable as a complex function it is said to be a complex analytic function or a holomorphic function.

Differentiability as a complex function is defined in the usual way as a limit:

f'(x) = \lim_{x\to X}\frac{f(x)-f(X)}{x-X}\,

but the epsilon-delta definition of the limit has to be interpreted very carefully. When we say 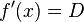$f'(x) = D\,$ , that is,

D = \lim_{x\to X}\frac{f(x)-f(X)}{x-X}\,

we mean that, for every real ε > 0, there is a real δ > 0 (yes, ε and δ are real) such that

whenever x is any complex number with

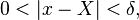
0 < |x-X| < \delta,\,

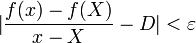
|\frac{f(x)-f(X)}{x-X} - D| < \varepsilon\,

This looks just like the usual "real" definition, except that the absolute values are taken on complex numbers. (The absolute value of a complex number is just its modulus, that is, its distance from the origin. It is a real number.)

Now 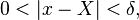$0 < |x-X| < \delta,\,$ means that x can be any complex number within the circle of radius δ, centered on X. This means that, when taking limits of complex numbers,

\lim_{x\to X}\,

x can approach X from any direction in the complex plane, not just from the left or right as with real limits.

This extra requirement on the limit that defines a complex derivative places strong constraints on differentiability. It is what makes these functions so powerful. A differentiable complex function is also called a complex analytic function or a holomorphic function. Among the remarkable properties of such functions are:

If it is differentiable, its derivative is also differentiable, so it is differentiable any number of times.
At any point in an open region in which a function is differentiable, its power series (Taylor series) about that point converges to the function.

This is actually the more general "official" definition of "analytic"—that the power series converges to the function. Functions on the real numbers can have this convergence property too—they are called "real analytic functions". But there are real functions that are differentiable but not real-analytic, such as

e^{-1/x^2}\,

Complex functions don't have this problem. If it is complex differentiable, it is complex analytic.

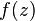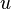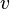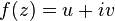The real and imaginary parts of a complex analytic function obey the Cauchy-Riemann Equations. If we represent the complex function $f(z)\,$ by real-valued functions $u$ and $v$ : $f(z) = u + i v\,$ , and furthermore represent those as functions of two real arguments which are the real and imaginary parts of 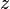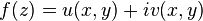$z$ : $f(z) = u(x, y) + i v(x, y)\,$ , we have:

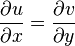\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}

and

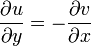
\frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}

If a complex analytic function doesn't go to infinity anywhere in the complex plane, even at infinity, that function is constant. This remarkable result is Liouville's theorem.

When a function goes to infinity at some point, that point is called a singularity. Singularities are often of a special type called a pole.

The real function

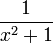
\frac{1}{x^2+1}\,

is not constant, and doesn't go to infinity for any real arguments. But it does go to infinity (it has poles) at

\pm i

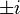A complex analytic function is completely determined by its values on any line segment anywhere on the complex plane. So, for example, if we know that a function matches the exponential function just on the real line, we know its value everywhere. That function is the "complex exponential". Similar extensions can be made for other real-analytic functions. That is, there are natural definitions for the complex sine, arctangent, logarithm, etc.
The power series for a complex analytic function converges (to the function itself, of course) on the interior of a circle around the point at which it is evaluated. That circle is the circle of convergence, with the radius of convergence. Outside of that circle, the series diverges. That doesn't mean the function isn't defined beyond that circle, just that that particular series fails. One can usually expand a power series around some other point to get the value of the function elsewhere. This is called analytic continuation.
The circle of convergence for a power series expansion just touches the nearest singularity. That is, the circle is the largest circle that does not contain any singularities.

This gives us insight into something about the real power series for the real arctangent function. A little calculation will show that, along the imaginary axis,

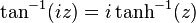\tan^{-1}(iz) = i \tanh^{-1}(z)\,

But the

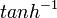tanh^{-1}\,

function has singularities at

\pm 1\,

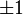, because

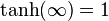\tanh(\infty) = 1\,

and

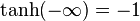\tanh(-\infty) = -1\,

Therefore, the

tan^{-1}\,

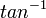function has singularities at

\pm i\,

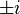, so the radius of convergence of its power series around the origin is 1. Even restricting one's attention to real numbers, the power series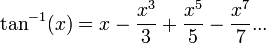

\tan^{-1}(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} ...\,

diverges beyond x=1.

Revisiting the complex generalization of the exponential function, its power series is:

\exp(z) = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \frac{z^4}{4!} + \frac{z^5}{5!} ...\,

Setting

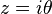z = i \theta\,

, we have

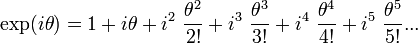
\exp(i\theta) = 1 + i \theta + i^2\ \frac{\theta^2}{2!} + i^3\ \frac{\theta^3}{3!} + i^4\ \frac{\theta^4}{4!} + i^5\ \frac{\theta^5}{5!} ...\,

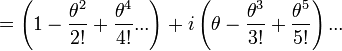
= \left(1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} ... \right) + i \left(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!}\right) ...\,

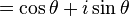= \cos\theta + i \sin\theta\,

from the known power series for the sine and cosine functions. So

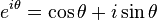
e^{i\theta} = \cos\theta + i \sin\theta\,

and Euler's famous formula, so mystifying when first seen:

e^{i\pi} = -1\,

This article is issued from Wikiversity - version of the Sunday, April 03, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.