Complex Analysis/Sample Midterm Exam 2
< Complex Analysis1. Restrict 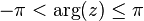 , and take the corresponding branch of
the logarithm:
, and take the corresponding branch of
the logarithm:
- a.
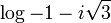
- b.
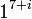
- c. Find all 4 roots of
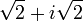
- d
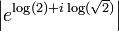
2. State the Cauchy-Riemann equations for a complex valued function 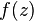 . If you use symbols other then
. If you use symbols other then  and
and 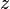 indicate how they relate to these quantities.
indicate how they relate to these quantities.
3. State whether the give function is holomorphic on the set where it is defined.
- a.
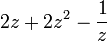
- b. Let
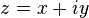 and let
and let 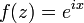 .
. - c.
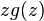 where
where 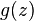 satisfies
satisfies 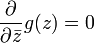
- d.
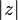
4. Let ![\gamma:[a,b]\to \C](../I/m/f03a4a82542620361f01f2d068a84de1.png) be a simple closed curve so that
be a simple closed curve so that  lies in the interior of the region bounded by
lies in the interior of the region bounded by 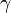 .
.
- a. Suppose
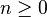 and compute
and compute 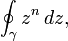
- simply writing the correct value without any explanation will not receive credit.
- b. We now consider the case corresponding to
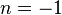 . Please compute
. Please compute 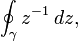
- and explain your steps.
- c: Now suppose
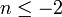 and compute
and compute 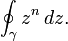
5. Let ![\gamma:[0,2\pi]\to \C](../I/m/c76ba60b21f55d0f23a352d2f2f5787d.png) be given by
be given by 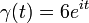 . Calculate
. Calculate 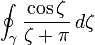
6. Let 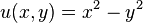 find a function
find a function 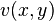 so that
so that 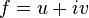 is holomorphic in the complex plane and
is holomorphic in the complex plane and 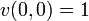 .
.
7.
- a. Using the limit characterization of the complex derivative show that
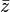 is not holomorphic.
is not holomorphic. - b. On the other hand show that if
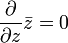 .
. - c. Do parts (a) and (b) contradict each other, explain why or why not.
8. State Cauchy's integral theorem, and intuitively what you need to know about the function, domain and contour.
This article is issued from Wikiversity - version of the Saturday, November 19, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.