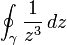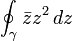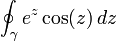Complex Analysis/Sample Midterm Exam 1
< Complex AnalysisThis exam has a total of 100 points. You have 50 minutes. Partial credit will be awarded so showing your work can only help your grade
Question 1: Restrict 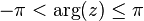 , and take the corresponding branch of the logarithm:
, and take the corresponding branch of the logarithm:
- (a)

- (b)
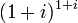
- (c)
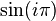
- (d)
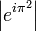
Question 2: Compute the following line integrals:
- (a) Let
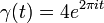 for
for ![t \in [0, 1]](../I/m/d9a06fde4663cdd5b1ba693e9127232f.png) . Compute the line integral
. Compute the line integral
- (b) Let
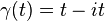 for
for ![t\in [0,1]](../I/m/d9a06fde4663cdd5b1ba693e9127232f.png) . Compute the line integral
. Compute the line integral
- (c) Let
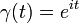 for
for ![t \in [0, 2\pi]](../I/m/10e9ceb4f0ea47ca0bfef8df01b9ae3b.png) . Compute the line integral
. Compute the line integral
Question 3: Let 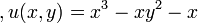 , verify that
, verify that 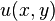 is harmonic
and find a function
is harmonic
and find a function 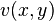 so that
so that 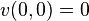 and
and 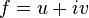 is a
holomorphic function.
is a
holomorphic function.
Question 4: Explain why there is no complex number 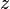 so that
so that 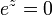 .
.
Question 5: We often use the formulas from ordinary calculus to compute complex derivatives. This problem is part of the justification. Show that if 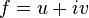 is holomorphic then
is holomorphic then 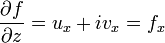 .
.
Comment: This problem shows that if 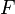 and
and  is a function in the complex plane, and
is a function in the complex plane, and 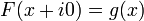 and
and 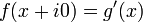 , then we can use this problem to show that
, then we can use this problem to show that 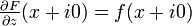 . We will
see later that if two holomorphic functions agree on a line then they agree everywhere. So it would have to be the case that
. We will
see later that if two holomorphic functions agree on a line then they agree everywhere. So it would have to be the case that
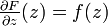 . (For example, take
. (For example, take 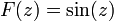 and
and 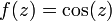 then
then 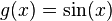 , so it must be that
, so it must be that 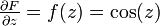 .)
.)
Question 6: Decide whether or not the following functions are holomorphic where they are defined.
- (a)
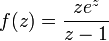
- (b)
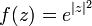
- (c) Let
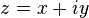 and let
and let 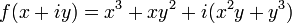
- (d) Let
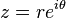 and let
and let 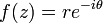
- (e) Let
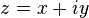 and let
and let 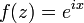
Question 7: State 4 ways to test if a function 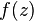 is holomorphic.
is holomorphic.