Cold fusion/Theory/Martin Gibson

moved from User talk:Martin Gibson permanent link. Otherwise unattributed text on this page is by Martin Gibson. Comments here by others may be refactored at Martin's approval or discretion. --Abd (discuss • contribs) 18:04, 1 May 2015 (UTC)

Cold Fusion Response

This is an attempt to address some of the questions raised by the the anomalous heat results of the Fleischmann-Pons experiment with palladium hydride and subsequent similar experiments and posed at the Wikiversity Cold fusion/Theory page. As indicated in the article on cold fusion in Wikipedia and a similarly named one on Wikiversity and elsewhere, the experiment involved the electrolysis of heavy water, with a wire of palladium at the cathode. The experiment resulted in an excess of output energy over the electrical input and outputs of possible chemical reactions, leaving the logical choices of experimental error or nuclear fusion reaction as the source of the heat.

Results expected to accompany conventional nuclear fusion would be the production of high energy and unstable helium, He-4*, with energy release, followed by decay by one of three pathways,

1. to produce a neutron and He-3 with energy,
2. to produce a proton and H-3, tritium with energy or
3. for the helium atom to emit a gamma ray.

The probability of the first two paths is closely 50% each, while the last is roughly 6 orders of magnitude less.

The experimenters reported small amounts of neutrons and of tritium, results indicative of pathways (1) and (2). Subsequent experiments by others have showed a high correlation of heat and He-4 indicative of nuclear fusion, but generally without the attendant gamma rays that would be expected by pathway (3). Such results suggest a mechanism for fusing hydrogen and/or deuterium to form stable helium in a manner that avoids radiation. Such mechanism lies outside established theory of nuclear interaction.

The following explanation of these results is offered for consideration and discussion:

Paladium and Nickel Crystal Structure

The catalysts in these experiments have been metals of the Group 10 elements, primarily palladium and some nickel, which have a crystall structure of the face-centered cubic (fcc) configuration, as can be seen at any of these links. A unit cell of such configuration is shown with dots representing the nucleus of each atom at each of the 8 vertices and at the center of each of the 6 surfaces of the cube.

Face centered cubic lattice - The blue dots represent the atomic nuclei, not to scale.

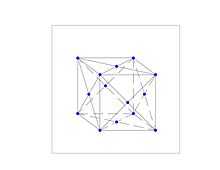
While this is instructive, it leaves the relationship of the coulomb force and the atomic binding force in the crystal to mathematical formulation, without the graphic representation which would help to understand what is going on in the catalyst of the experimental setup. We will assume that the atomic bonding in the lattice is covalent and scaled as determined by a covalent radius of 124(4) picometers(pm) for nickel and of 139(6) pm for palladium atoms, so that center to center of the nuclei, as from the center face node to vertex node, is twice that value in each case or 248 pm for the nickel and 278 pm for the palladium, disregarding the statistical uncertainty. The unit cell edge is then the square root of 2 times these values (since 2 divided by the square root of 2 equals the square root of 2).

Both elements have 10 valence electrons. The nickel electron configuration is [Ar]3d⁸4s² or [Ar]3d⁹4s¹ and the palladium configuration is [Kr]4d¹⁰. With respect to palladium, it is significant that it has no 5s orbital as do the preceding transition metals in period 5. It is also important that both hydrogen and palladium have the same electronegativity on the Pauling scale of 2.20.

It is noted that the configuration of the face centered cube is listed as the maximum or densest form of packing of like sized spheres with a packing efficiency of 74% and that there is no atom in the center of this unit cell.

Lattice geometry

From this arrangement we can construct the configuration shown below which I refer to as a cuboctahedral lattice and which is identical to the fcc. In place of the representation of an atomic nuclei by a dot, we have inserted equal sized spheres to represent the extent of the atom as determined by its covalent radius. In this case, however, one side of the cube has been left off and the four surface center points of the unit cell adjacent to the opposite surface side have been added. This leaves a sphere for the common cubic cell surface at the center of the cuboctahedron. This view shows the center of the conventional fcc, as an octahedral interstitial space, O, between the unit surface center spheres that is devoid of a lattice atom. For the conventional fcc, in addition to the center of the cube, the mid point of each of the edges constitutes a similar vacant point. An extended crystal lattice of similar unit cells is in reality a lattice of interlocking cubic cells off set-from the first by half the edge length along each of three coordinate directions. Other than the boundary condition, there is one O for each of the metallic atoms in the lattice.

A cuboctahedral lattice which is the same structure as the face centered cubic lattice. Here the nodes have been replaced with spheres representing the covalent radii of the lattice atoms.

The octahedral chamber between lattice atoms - this is the interstitial area in the surface of the lattice where hydrogen is absorbed.

This aperture leads to the tetrahedral chamber. In the palladium lattice, this chamber is within one picometer of the size of the hydrogen covalent radius times 2.

Using the covalent radii for nickel and palladium, we can determine that the free space in the Os is sufficient to allow absorption of a sphere of maximum radius of 51pm and 57.5 pm respectively. The covalent radius of hydrogen is 31(5) pm. Thus the octahedral space appears to be adequate for the containment of absorbed hydrogen.

It can be seen in the cuboctahedral photo that in addition to the large, octahedral apertures on the surface of the structure, which in the interior of an extension of such lattice become octahedral chambers, O, there are smaller triangular openings. These tetrahedral apertures lead to a tetrahedral shaped interstitial space, T, defined by 4 joining, tetrahedral configured spheres. On the conventional fcc, these spheres are represented by the nodes at each vertex and the adjacent nodes at the 3 proximal surface centers, keeping in mind that each surface node can be a vertex node for one of the other interlocking cell configurations. There are 4 tetrahedral apertures with connecting chambers leading from any exterior octahedral aperture to the interior and 8 of these leading from any interior octahedral space to another such octahedral space. Thus there are 4 octahedral spaces that can be accessed from each tetrahedral space.

The tetrahedral aperture will admit a sphere of 19.2 pm radius for the nickel and 21.5 pm radius for the palladium lattice. The tetrahedral chamber will circumscribe a sphere of radius 27.86 pm for the nickel and 31.24 pm for the palladium lattice. Thus the chamber allows for an increase in radius of 1.45 times the aperture allowance. Based on the covalent radius within the statistical uncertainty, an atom of hydrogen would fit snuggly inside the T chamber of either the nickel or palladium lattice, as would the helium.

It is observed that palladium as a transition metal hydride catalyst, readily admits the diffusion of hydrogen through the lattice and that if the palladium adheres to this fcc/cuboctahedral configuration in some manner of covalent bonding, this of necessity must result in conduction of hydrogen through the tetrahedral interstitial chambers.

What appears to be going on?

The following would appear to be the mechanism for the experimental results of low energy nuclear reaction based on the analysis of the lattice geometry. H or hydrogen will refer to D, deuterium and tritium, unless stated otherwise.

• A palladium catalyst absorbs hydrogen at room temperature to form palladium hydride filling up to approximately 70% of the octahedral chambers in the lattice.
• The palladium atom valence electrons are comprised of the 4d¹⁰ orbitals which are full. The d_{xy}, d_{xz}, and d_{yz} orbitals apparently establish the fcc or cuboctahedral configuration of the lattice, bonding to the adjacent 12 palladium atoms, and the d_{x²-y²} and one orbital of d_{z²} provide a potential for covalent bonding to hydrogen in the O chambers. This leaves an electron in the remaining d_{z²} toric orbital, which with minor energy input can jump to the 5s orbital.
• In the O chambers, entering H or D forms a covalent bond with one of the palladium atoms. In the case of H^- or D^-, two bonds are formed with adjacent palladium atoms. As both palladium and hydrogen have the same electronegativity of 2.20 on the Pauling scale and assuming its applicability in the interstitial areas of the lattice, the hydrogen nucleus will maintain the same distance from the covalent bond as the palladium nucleus, a distance equal to the palladium covalent radius. The Pauli exclusion principle requires that the hydrogen nucleus remain in the interstitial area of the O or T chambers.

1. For a covalent bond with one of the four proximal (of the total five) atoms that define a surface O chamber, there are four positions the hydrogen nucleus can take, in the center of the four tetrahedral apertures on the far side of the O chamber. These positions are in the planes of the nuclei of the corresponding three lattice atoms forming the apertures. In the case of lattice interior O chambers which have six boundary atoms, there are 8 apertures but only 4 positions with respect to any covalent bond formed with a Pd d_{x²-y²} or d_{z²} electron orbital. As the covalent bond is established, the hydrogen nucleus positions itself in the interstitial region the same distance from the covalent bond as the Pd nucleus is to the other side. The only possible space is one of the four T distal apertures, where the coulomb force centers it in the opening. In the case of hydride the possible positions are reduced to two distal apertures.
2. As a consequence of the Coulomb force, the proximity of the nucleus to the aperture atoms can lead to the breaking of the covalent bond(s) on the far side of the O chamber and entry of the H nucleus into the T chamber, and in some cases through into one of the adjacent O chambers and a repetition of the previous covalent bonding step.
3. In the absence of an excitation of the four palladium atoms forming the T chamber, i.e. the absence of a 5s orbital, there will be no potential for covalent bonding in that chamber and the hydrogen can come to rest therein, with its nucleus at the center.
4. In the event of another hydrogen entering the chamber and the availability of an open adjacent O, the H will exit and repeat the covalent bonding step.
5. With excitation of the 5s orbital of one or more of the tetrahedral Pd, the H can form a covalent bond and electronegativity functions to project the H nucleus into another adjacent O chamber through the distal aperture, where once again the covalent bond transfers to one of the three aperture lattice atoms behind the nucleus.
6. Electronegativity again projects the nucleus to one of four distal apertures across the O chamber.
7. In the case of a hydride, with bonds to two adjacent atoms, projection of the nucleus from the T chamber is impeded by the tetrahedral geometry, though entry of another nucleus in the absence of exit obstructions will eject the H^-.
8. We would anticipate that under conditions of electrolysis in which the palladium is at the cathode, intrusion of H^- will be mitigated.
9. In this manner the hydrogen readily diffuses through the palladium, without reaching the density required for fusion. In the event this process causes two atoms of hydrogen to attempt to enter the same chamber, electrostatics will cause one of them to divert to another chamber or exit the lattice.

• Electrolysis increases the loading of the interstitial chambers with hydrogen or deuterium, by creating a gradient at the surface of the lattice.
• As the O chambers become loaded, pressure from the filled O chambers prevents movement of hydrogen out of the T chambers so that we can expect absorption of hydrogen in excess of the O chamber availability or in excess of 100% as it will include some of the T chambers.
• As just described, forming a covalent bond in the O chamber creates an elongation of the H atom, resulting in entry into the T chamber.
• In the case of a palladium lattice, the T chamber capacity is for a sphere of the the same covalent radius as H₂. In the case of a nickel lattice it is approximately 3 pm smaller.
• As a reference, Muon-catalyzed fusion relies on the increased mass of the muon to confine the nuclei of the fusion components by 207 times their normal separation at ambient temperature. This factor represents a reduction in the covalent radius of hydrogen to about 0.15 pm. Here that value represents a “sweet spot” in the center of the tetrahedral chamber or aperture of that radius.
• From the above we can postulate two paths for fusion:

1. In a condition of absorption saturation of the lattice, an atom of hydrogen in the T chamber is prevented from entering an occupied adjacent O chamber by electrostatics of the occupant and will tend to center in the T chamber after entry in response to the Coulomb forces in the T chamber . There its nucleus is positioned for collision with any hydrogen nucleus that follows from any of the four apertures. Formation of a covalent bond with one of the four lattice atoms of the T chamber by another H entering the chamber, will result in the rotation of its nucleus toward the the center of the T chamber and its projection through the distal aperture.
2. As the loading increases, the likelihood increases for the coincidence of a electronegativity extension of a hydrogen nucleus to a T aperture center followed simultaneously by a similar extension of an H nucleus through that same point from within the T chamber.

• In the case of two deuterium atoms, with the coming together of the nuclei, the neutron in each nucleus helps shield the proton from the proton in the other nucleus.
• Nuclear bonding thereby occurs in the T chamber or aperture center, with a reduction in spin energy, i.e. mass, of the nucleons, and that energy is transferred to the adjacent lattice as heat motion without the need for a quantum emission, i.e. a gamma ray. Such energy also elevates the energy of a 4d electron to 5s, enhancing the capacity of the T chambers for covalent bonding and additional fusion reactions.
• As an atom of He-4 is produced, the 1s² shell is filled by two electrons previously coupled in the covalent bond, freeing it molecularly from the lattice. Momentum from the nuclear collision and the increased lattice energy ejects the helium from the T chamber into an adjacent O chamber, and if it is near the surface of the catalyst, into the electrolyte.
• If charge of the cathode is instrumental in initiating and sustaining entrance into and movement through the interior of the catalyst and the current is generally confined to the surface of the catalyst, it follows that the reactions will tend to occur in the surface regions of the catalyst, once the interior is packed to a saturation level.
• The heat produced by this mechanism will be commensurate with the fusion products produced but will involve molecular heating of the reactor system, by conduction and convection, and not primarily radiant heating.

Summary

The arrangement of the lattice of nickel and palladium catalysts produces geometric constraints, along with special orbital and electronegativity configurations in the case of palladium, that under conditions of loading of the lattice interstitial areas with hydrogen as under electrolysis of heavy and to some degree light water, confines the fusion fuel to the pico and femto scale to allow the production of heavy hydrogen and helium with the attendant release and transfer of spin energy to the lattice in the form of conductive heat. Understanding of this configuration should be of benefit in design of the catalyst, including the introduction of possible alloys and doping techniques.

Theoretical Context

While it is perhaps not necessary for an understanding of this development, the matter is facilitated if the fundamental massive particles, neutron, proton and electron are modeled as discrete inertially constrained oscillations of a spatial inertial continuum-substrate, as this writer has investigated elsewhere. That investigation suggests the emergence of lattice structures such as just described in response to stress and strain associated with expansion of that space. It also offers insights into and a better understanding of the coulomb force.

Comments

• Nice study of the crystal geometry. I still have trouble wrapping my head around it. Classically, it was thought that loading above 70% (i.e., 7 hydrogen/deuterium atoms per 10 palladium) was impossible. Hence the early replication failures occurred when investigators believed that 70% loading or so was enough. McKubre has written that he was already familiar with loaded PdD -- as were many, and anomalous heat effects had not been observed, so he knew that Pons and Fleischmann must have moved above 70%, in an unexplored territory. In fact, as later work has shown, the FP Heat Effect does not begin to show up until well over 80%, and few results have less than 90% loading.

• There is an experimental fact you have not absorbed. Helium is immobilized in Pd. It will, indeed, move through the lattice -- slowly by comparison with H/D -- , but is trapped at grain boundaries, which has been shown by studies with PdT. Tritium decays to 3He, which will then be distributed through the lattice. Except for He very near the surface, it stays in the lattice, accumulating if generation continues.

Yet from the FP Heat Effect, helium is not found in the lattice, beyond the surface layer. Morrey et al, in 1989, removed the top 25 microns and found no helium in what remained. The helium that is found is at about 60% of theoretical from fusion, indicating about 40% retained. Damage to the outer layer using reverse electrolysis has resulted in the recovery of all the helium, apparently.

If helium were generated by a simple mechanism operating in normal lattice, almost all of it would be retained, instead of about 40%, and it would only be removed by melting the palladium or by dissolving it all.

Hence to apply to the actual effect, a mechanism must work under surface conditions, and not in the pure lattice. The environment that catalyzes the reaction must, as well, be special, not just ordinary surface, because of a basic characteristic of the FP Heat Effect: its famous unreliability. That is almost certainly due to aging of the surface, changes that take place over time, and that only result transiently in the necessary conditions. Storms terms the "necessary conditions" as the Nuclear Active Environment (NAE), and suggests, as NAE, very small surface cracks, termed "nanocracks," they are probably less than a nanometer wide, in his theory, which requires that molecular hydrogen (H2 or D2) be excluded. Other theories might work with somewhat wider cracks, and suggest that molecular hydrogen is involved, but it's also obvious that confinement is involved.

• My own cold fusion theory is "it's a mystery." That means, to me, an opportunity. We probably need more data to go further than we have. But that deuterium is being converted to helium, without high-energy gammas, in the FPHE, is conclusive from the evidence, see my review. I would not say "beyond doubt," but it's very strong. --Abd (discuss • contribs) 18:04, 1 May 2015 (UTC)