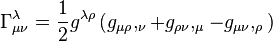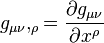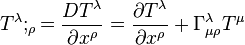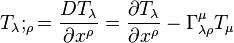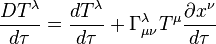Christoffel symbols
| | Resource type: this resource contains a lecture or lecture notes. |
|
The Christoffel symbols are related to the metric tensor by
|
|
where the comma is a partial derivative. For example
|
|
The Christoffel symbols are part of a covariant derivative opperation, represented by a semicolin or capitalized D ,mapping tensor elements to tensor elements. For example
|
|
Also for example
|
|
And differentiating with respect to an invariant example
|
|
References
This article is issued from Wikiversity - version of the Saturday, January 18, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.