Cauchy Theorem for a triangle
Theorem
Let 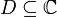 be a domain,
be a domain, 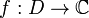 a differentiable function. Let
a differentiable function. Let 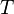 be a triangle such that
be a triangle such that 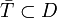 . Then
. Then
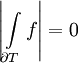
Proof
Assume
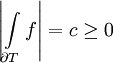 .
.
It will be shown that 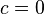 .
.
First, subdivide  into four triangles, marked
into four triangles, marked 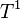 ,
, 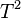 ,
, 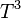 ,
, 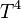 by joining the midpoints on the sides. Then it is true that
by joining the midpoints on the sides. Then it is true that
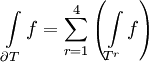 .
.
Giving that
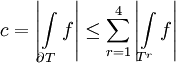
Choose  such that
such that
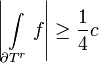
Defining  as
as 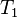 , then
, then
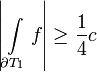 and
and 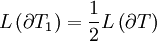
(where 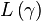 describes length of curve).
describes length of curve).
Repeat this process of subdivision to get a sequence of triangles
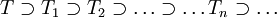
satisfying that
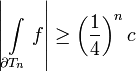 and
and 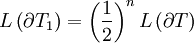 .
.
Claim: The nested sequence 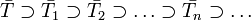 contains a point
contains a point 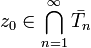 . On each step choose a point
. On each step choose a point 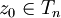 . Then it is easy to show that
. Then it is easy to show that 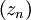 is a Cauchy sequence. Then
is a Cauchy sequence. Then 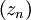 converges to a point
converges to a point 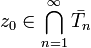 since each of the
since each of the 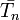 s are closed, hence, proving the claim.
s are closed, hence, proving the claim.
We can generate another estimate of  using the fact that
using the fact that  is differentiable. Since
is differentiable. Since  is differentiable at
is differentiable at 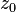 , for a given
, for a given 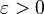 there exists
there exists 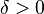 such that
such that
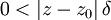 implies
implies 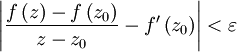
which can be rewritten as
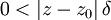 implies
implies 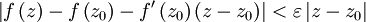
For 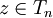 we have
we have 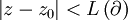 , and so, by the Estimation Lemma we have that
, and so, by the Estimation Lemma we have that
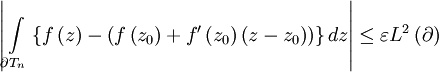
As 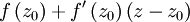 is of the form
is of the form 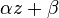 it has an antiderivative in D, and so
it has an antiderivative in D, and so 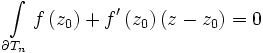 , and the above is then just
, and the above is then just
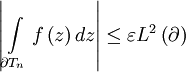
Notice that
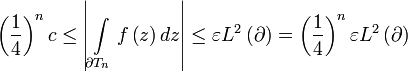
Giving
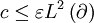
Since 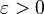 can be chosen arbitrary small, then
can be chosen arbitrary small, then 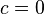 .
.