Cauchy-Riemann Equations
Theorem
Let 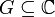 be an open subset. Let the function
be an open subset. Let the function 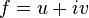 be differentiable at a point
be differentiable at a point 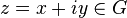 . Then all partial derivatives of
. Then all partial derivatives of 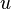 and
and 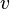 exist at
exist at 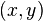 and the following Cauchy-Riemann equations hold:
and the following Cauchy-Riemann equations hold:
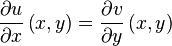
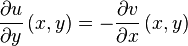
In this case, the derivative of  at
at 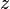 can be represented by the formula
can be represented by the formula
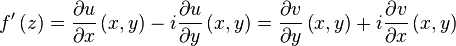
Proof
Let 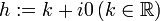 . Then
. Then
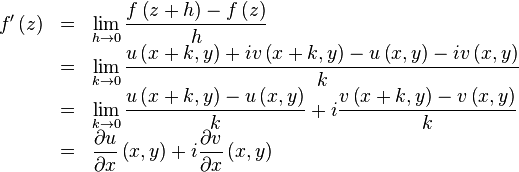
Let 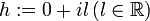 . Then
. Then
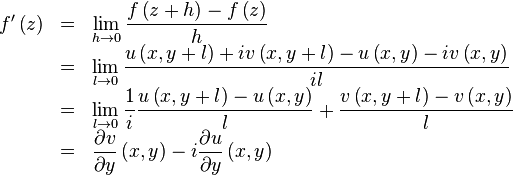
Hence:
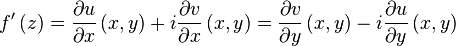
Equating the real and imaginary parts, we get the Cauchy-Riemann equations. The representation formula follows from the above line and the Cauchy-Riemann equations.
This article is issued from Wikiversity - version of the Tuesday, October 08, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.