Category
Category, in mathematics, is a fundamental, algebraic or topological (super-, or meta-) structure formed by objects connected through arrows or morphisms into (categorical) diagrams, that has an identity arrow for each object, and is subject to certain axioms of associativity, commutativity and distributivity. The objects of a category can be simple sets, or specific algebraic structures such as monoids, w:semigroups, groups, groupoids, rings, modules, lattices, or topological structures, such as a topological space/ a graph/ a network, a meta-graph, and so on.
Category definition
A category can be defined in several equivalent ways, as follows.
Definition #1: A category 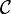 consists of
consists of
- A set
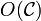 of objects.
of objects.
- A set
- For any
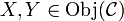 , a set
, a set 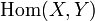 of morphisms from
of morphisms from  to
to 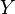 .
.
- For any
The objects and morphisms of a category obey the following defining axioms:
- There is a notion of composition. If
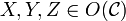 ,
, 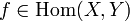 and
and 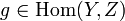 , then
, then  and
and 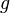 are called a composable pair. Their composition is a morphism
are called a composable pair. Their composition is a morphism 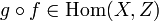 .
.
- There is a notion of composition. If
- Composition is associative.
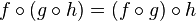 whenever the composition is defined.
whenever the composition is defined.
- Composition is associative.
- For any object
 , there is an identity morphism
, there is an identity morphism 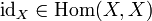 such that if
such that if 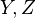 are objects,
are objects, 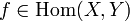 and
and 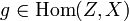 , then
, then 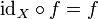 and
and 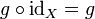 .
.
- For any object
Definition #2: A morphism  has associated with it two functions
has associated with it two functions 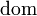 and
and 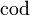 called domain and codomain respectively, such that
called domain and codomain respectively, such that 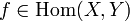 if and only if
if and only if 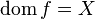 and
and 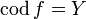 . Thus two morphisms
. Thus two morphisms 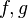 are composable if and only if
are composable if and only if 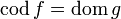 .
.
Remark 3: Unless confusion is possible, one will not usually specify which Hom-set a given morphism belongs to. Moreover, unless several categories are being considered, one usually does not write completely 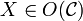 , but writes instead as a short-hamd notation: "
, but writes instead as a short-hamd notation: " is an object". One may also write
is an object". One may also write 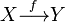 to indicate implicitly the Hom-set
to indicate implicitly the Hom-set  to which it belongs to. Furthermore, one may also omit the composition symbol "o" , writing simply
to which it belongs to. Furthermore, one may also omit the composition symbol "o" , writing simply 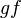 instead of
instead of 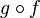 .
.
- A category can also be regarded as a "<structure> of structures of the same mathematical kind, connected via their transformations or homomorphisms/ homeomorphisms". A "<category> of categories" can also be defined for small categories; it is usually called a super-category. The objects of a super-category are categories of any kind, and the arrows of a super-category are called w:functors. One can also define arrows between functors that are called natural transformations, and the essence of the mathematical theory of categories. or Category Theory, is often contained in natural transformations, such as natural equivalences.
- A proposed, logical axiomatics for categories was proposed by William F. Lawvere in the form of the Elementary Theory of Abstract Categories (ETAC), in which identities, objects, arrows, associativity, commutativity and distributivity properties are defined in logical terms and logical connectives.
- A groupoid, for example, can be considered as a category with all arrows being invertible. It is possible alos to endow an algebraic structure, such as a group, or groupoid, with a (consistent) topological structure. An example of a group endowed with a topological structure is a Lie group that plays an important role in quantum physics; its generalization to many objects is a topological groupoid called a Lie groupoid, which has more complex mathematical properties than the Lie group.
See also
For information on Wikiversity categories see Wikiversity: Categories.