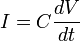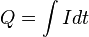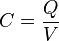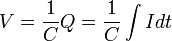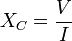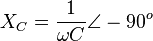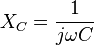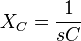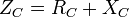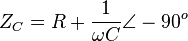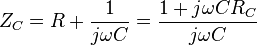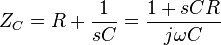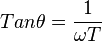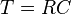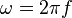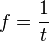Capacitor

Resource type: this resource is an article.
Subject classification: this is a physics resource .
Subject classification: this is an engineering resource .
Educational level: this is a secondary education resource.
Educational level: this is a tertiary (university) resource.

A capacitor is an electronic component designed to obey the equation:

I = C \frac{dV}{dt}\,

See Introduction to Electricity II for theoretical details about capacitors.

The current that an ideal capacitor "passes" through it depends on the rate of change of the voltage applied across it. The direction of the current will be in such a way as to counteract the change of voltage. A capacitor is not the same as a battery. A capacitor stores energy through charge and battery stores energy through a chemical change. The fundamental prototype of a capacitor consists of two conducting parallel plates separated by an insulating material called the dielectric.

Factors affecting capacitance

Uses of the capacitor

Real capacitors have non-zero DC leakage current, non-zero lead resistance and inductance, memory behavior etc. Capacitor Symbol

Charge Stored

Q = \int I dt

Capacitance

The capability of a capacitor to store charge of a voltage

C = \frac{Q}{V}

Voltage

V = \frac{1}{C} Q = \frac{1}{C} \int I dt

Reactance

X_C = \frac{V}{I}
X_C = \frac{1}{\omega C} \angle -90^o
X_C = \frac{1}{j \omega C}
X_C = \frac{1}{sC}

Impedance

Z_C = R_C + X_C
Z_C = R + \frac{1}{\omega C} \angle -90^o
Z_C = R + \frac{1}{j \omega C} = \frac{1 + j \omega CR_C}{j \omega C}
Z_C = R + \frac{1}{s C} = \frac{1 + s CR}{j \omega C}

Frequency Response

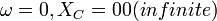\omega = 0, X_C = 00 (infinite) . DC Applied, capacitor is an open circuit , I = 0
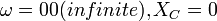\omega = 00 (infinite), X_C = 0 . HF AC applied, capacitor is a short circuit , I - limited by rest of circuit
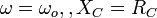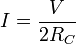
\omega = \omega_o, ,X_C = R_C . I = \frac{ V}{2R_C}

With Current's values at three point 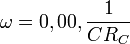\omega = 0, 00 ,\frac{1}{CR_C} a I - ш can be drawn.

Phase Angle

For capacitor without resistance, Voltage and current have a phase difference of 90o

For capacitor with resistance, Voltage and current have a phase difference of θ

Tan \theta = \frac{1}{\omega T}
T = RC
\omega = 2 \pi f
f = \frac{1}{t}

See also

This article is issued from Wikiversity - version of the Friday, September 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.