Calculus/Derivatives
< Calculus Derivative of a function  at a number
at a number 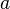
Notation
We denote the derivative of a function  at a number
at a number 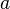 as
as 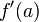 .
.
Definition
The derivative of a function  at a number
at a number 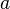 a is given by the following limit (if it exists):
a is given by the following limit (if it exists):
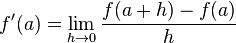
An analagous equation can be defined by letting 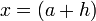 . Then
. Then 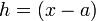 , which shows that when
, which shows that when  approaches
approaches 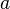 ,
, 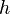 approaches
approaches 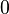 :
:
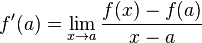
Interpretations
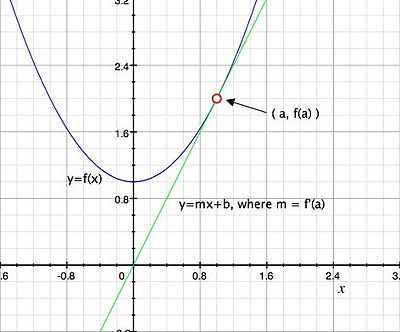
As the slope of a tangent line
Given a function 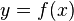 , the derivative
, the derivative 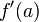 can be understood as the slope of the tangent line to
can be understood as the slope of the tangent line to  at
at  :
:
Example
Find the equation of the tangent line to 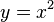 at
at 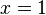 .
.
Solution
To find the slope of the tangent, we let 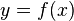 and use our first definition:
and use our first definition:
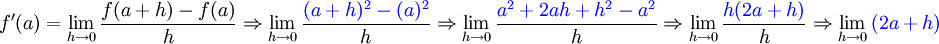
It can be seen that as 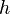 approaches
approaches 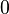 , we are left with
, we are left with 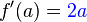 . If we plug in
. If we plug in 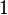 for
for 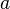 :
:
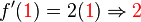
So our preliminary equation for the tangent line is 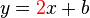 . By plugging in our tangent point
. By plugging in our tangent point 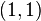 to find
to find 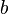 , we can arrive at our final equation:
, we can arrive at our final equation:
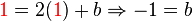
So our final equation is 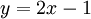 .
.
As a rate of change
The derivative of a function  at a number
at a number 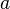 can be understood as the instantaneous rate of change of
can be understood as the instantaneous rate of change of  when
when  .
.
The derivative as a function
So far we have only examined the derivative of a function  at a certain number
at a certain number 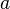 . If we move from the constant
. If we move from the constant 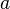 to the variable
to the variable  , we can calculate the derivative of the function as a whole, and come up with an equation that represents the derivative of the function
, we can calculate the derivative of the function as a whole, and come up with an equation that represents the derivative of the function  at any arbitrary
at any arbitrary  value. For clarification, the derivative of
value. For clarification, the derivative of  at
at 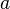 is a number, whereas the derivative of
is a number, whereas the derivative of  is a function.
is a function.
Notation
Likewise to the derivative of  at
at 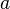 , the derivative of the function
, the derivative of the function  is denoted
is denoted 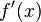 .
.
Definition
The derivative of the function  is defined by the following limit:
is defined by the following limit:
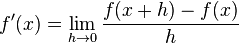
Also,
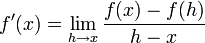
or
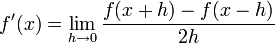
| Go to the School of Mathematics |