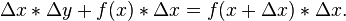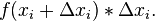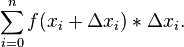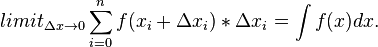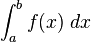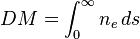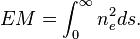Calculus
Calculus uses methods originally based on the summation of infinitesimal differences.
It includes the examination of changes in an expression by smaller and smaller differences.
Mathematics
Mathematics is about numbers (counting), quantity, and coordinates.
Def. "[a]n abstract representational system used in the study of numbers, shapes, structure and change and the relationships between these concepts"[1] is called mathematics.
Variations
Def. "a partial change in the form, position, state, or qualities of a thing"[2] or a "related but distinct thing"[2] is called a variation.
Differences
Def. "[s]ignificant change in or effect on a situation or state"[3] or a "result of a subtraction; sometimes the absolute value of this result"[3] is called a difference.
Notation: let the symbol 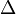 represent change in.
represent change in.
Notation: let the symbol 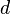 represent an infinitesimal change in.
represent an infinitesimal change in.
Notation: let the symbol 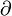 represent an infinitesimal change in one of more than one.
represent an infinitesimal change in one of more than one.
Derivatives
Def. a result of an "operation of deducing one function from another according to some fixed law"[4] is called a derivative.
Let
be a function where values of 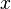 may be any real number and values resulting in
may be any real number and values resulting in 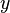 are also any real number.
are also any real number.
-
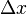 is a small finite change in
is a small finite change in 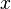 which when put into the function
which when put into the function 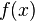 produces a
produces a 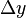 .
.
These small changes can be manipulated with the operations of arithmetic: addition (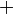 ), subtraction (
), subtraction ( ), multiplication (
), multiplication (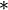 ), and division (
), and division (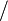 ).
).
Dividing 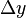 by
by 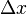 and taking the limit as
and taking the limit as 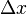 → 0, produces the slope of a line tangent to f(x) at the point x.
→ 0, produces the slope of a line tangent to f(x) at the point x.
For example,
as 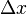 and
and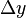 go towards zero,
go towards zero,
This ratio is called the derivative.
Partial derivatives
Let
then
where z is held constant and
where x is held contstant.
Gradients
Notation: let the symbol 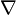 be the gradient, i.e., derivatives for multivariable functions.
be the gradient, i.e., derivatives for multivariable functions.
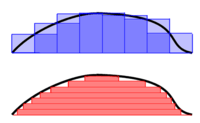
Area under a curve
For
the area under the curve shown in the diagram at right is the light purple rectangle plus the dark purple rectangle in the top figure
Any particular individual rectangle for a sum of rectangular areas is
The approximate area under the curve is the sum 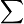 of all the individual (i) areas from i = 0 to as many as the area needed (n):
of all the individual (i) areas from i = 0 to as many as the area needed (n):
Integrals
Def. a "number, the limit of the sums computed in a process in which the domain of a function is divided into small subsets and a possibly nominal value of the function on each subset is multiplied by the measure of that subset, all these products then being summed"[5] is called an integral.
Notation: let the symbol 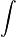 represent the integral.
represent the integral.
This can be within a finite interval [a,b]
when i = 0 the integral is evaluated at 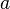 and i = n the integral is evaluated at
and i = n the integral is evaluated at 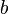 . Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
. Or, an indefinite integral (without notation on the integral symbol) as n goes to infinity and i = 0 is the integral evaluated at x = 0.
Theoretical calculus
Def. a branch of mathematics that deals with the finding and properties ... of infinitesimal differences [or changes] is called a calculus.
"Calculus [focuses] on limits, functions, derivatives, integrals, and infinite series."[6]
"Although calculus (in the sense of analysis) is usually synonymous with infinitesimal calculus, not all historical formulations have relied on infinitesimals (infinitely small numbers that are nevertheless not zero)."[7]
Line integrals
Def. an "integral the domain of whose integrand is a curve"[8] is called a line integral.
"The pulsar dispersion measures [(DM)] provide directly the value of
along the line of sight to the pulsar, while the interstellar Hα intensity (at high Galactic latitudes where optical extinction is minimal) is proportional to the emission measure"[9]
Research
Hypothesis:
- Calculus can be described using set theory.
Control groups

The findings demonstrate a statistically systematic change from the status quo or the control group.
“In the design of experiments, treatments [or special properties or characteristics] are applied to [or observed in] experimental units in the treatment group(s).[10] In comparative experiments, members of the complementary group, the control group, receive either no treatment or a standard treatment.[11]"[12]
Proof of concept
Def. a “short and/or incomplete realization of a certain method or idea to demonstrate its feasibility"[13] is called a proof of concept.
Def. evidence that demonstrates that a concept is possible is called proof of concept.
The proof-of-concept structure consists of
- background,
- procedures,
- findings, and
- interpretation.[14]
See also
References
- ↑ "mathematics, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. January 13, 2013. Retrieved 2013-01-31.
- 1 2 87.113.182.130 (14 April 2011). "variation, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 2015-06-25.
- 1 2 "difference, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. 28 May 2015. Retrieved 2015-06-25.
- ↑ Poccil (13 January 2015). "derivation, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. Retrieved 2015-06-25.
- ↑ "integral, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. 30 May 2015. Retrieved 2015-06-25.
- ↑ "Calculus, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. October 13, 2012. Retrieved 2012-10-14.
- ↑ "infinitesimal calculus, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. Setember 19, 2012. Retrieved 2013-01-31.
- ↑ "line integral, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. September 18, 2013. Retrieved 2013-12-17.
- ↑ R. J. Reynolds (May 1, 1991).
 . The Astrophysical Journal 372 (05): L17-20. doi:10.1086/186013. http://adsabs.harvard.edu/full/1991ApJ...372L..17R. Retrieved 2013-12-17.
. The Astrophysical Journal 372 (05): L17-20. doi:10.1086/186013. http://adsabs.harvard.edu/full/1991ApJ...372L..17R. Retrieved 2013-12-17. - ↑ Klaus Hinkelmann, Oscar Kempthorne (2008). Design and Analysis of Experiments, Volume I: Introduction to Experimental Design (2nd ed.). Wiley. ISBN 978-0-471-72756-9. http://books.google.com/?id=T3wWj2kVYZgC&printsec=frontcover.
- ↑ R. A. Bailey (2008). Design of comparative experiments. Cambridge University Press. ISBN 978-0-521-68357-9. http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=9780521683579.
- ↑ "Treatment and control groups, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. May 18, 2012. Retrieved 2012-05-31.
- ↑ "proof of concept, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. November 10, 2012. Retrieved 2013-01-13.
- ↑ Ginger Lehrman and Ian B Hogue, Sarah Palmer, Cheryl Jennings, Celsa A Spina, Ann Wiegand, Alan L Landay, Robert W Coombs, Douglas D Richman, John W Mellors, John M Coffin, Ronald J Bosch, David M Margolis (August 13, 2005). "Depletion of latent HIV-1 infection in vivo: a proof-of-concept study". Lancet 366 (9485): 549-55. doi:10.1016/S0140-6736(05)67098-5. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1894952/. Retrieved 2012-05-09.
External links
- African Journals Online
- Bing Advanced search
- Google Books
- Google scholar Advanced Scholar Search
- JSTOR
- Lycos search
- Office of Scientific & Technical Information
- Questia - The Online Library of Books and Journals
- SAGE journals online
- The SAO/NASA Astrophysics Data System
- Scirus for scientific information only advanced search
- SpringerLink
- Taylor & Francis Online
- Wiley Online Library Advanced Search
- Yahoo Advanced Web Search
![]() This is a research project at http://en.wikiversity.org
This is a research project at http://en.wikiversity.org
| |
Development status: this resource is experimental in nature. |
| |
Educational level: this is a research resource. |
| |
Resource type: this resource is an article. |
| |
Resource type: this resource contains a lecture or lecture notes. |
| |
Subject classification: this is a mathematics resource . |
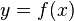
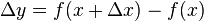
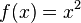
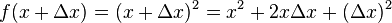
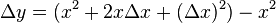
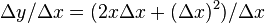
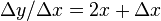
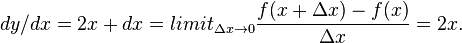
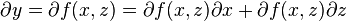
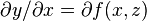
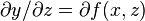
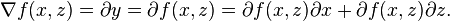
![\Delta x * \Delta y = [f(x + \Delta x) - f(x)] * \Delta x](../I/m/6da4993c799821d9a1d81ba4727956af.png)