Calculating the square root of a

In this learning project, we learn how to approximate the square root of a number numerically.

Newton's method

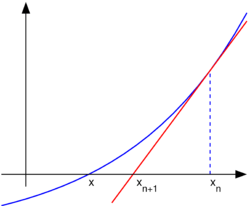
Newton's method is a basic method in numerical approximations. The idea of Newton's method is to "follow the tangent line" to try to get a better approximation. For more details, see w:Newton's method

Try your hand on Newton's method

Step-by-step

Cut and paste the following wikitext into the sandbox, and enter your favourite number and a first (non-zero!) approximation of its square root. See what happen after multiple edit-and-saves:

{{subst:square root|number|first approximation}}

Sandbox

{{subst:square root|17|4.1231056256177}}
4.1231056256177
4.1231056256177
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310877528
4.1282051282
4.33333333333
3

What is going on

Our calculator-template {{square root}} implements the formula 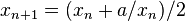$x_{n+1} = (x_n + a/x_n)/2$ , which is an instant of the general formula for Newton's method 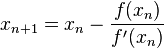$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\,\!$ in the case when the function f(x) is given by 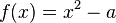$f(x)=x^2 - a$ . It solves the equation 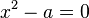$x^2 - a=0$ numerically, by successive approximations.

This article is issued from Wikiversity - version of the Tuesday, January 03, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.