Boundary Value Problems/Series Solutions

< Boundary Value Problems

In your Calculus course you were introduced to Power Series and the representation of certain types of functions using Taylor series.

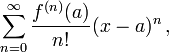$\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}\,,$ where n! is the factorial of n and f⁽ⁿ⁾(a) denotes the nth derivative of f evaluated at the point a; the zeroth derivative of f is defined to be f itself and (x − a)⁰ and 0! are both defined to be 1.

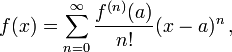
If the Taylor series converges to $f(x)$ we write $f(x)=\sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}\,,$

Return to Boundary Value Problems

This article is issued from Wikiversity - version of the Saturday, July 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.