Boundary Value Problems/Problem Lookup

< Boundary Value Problems

Click here to return to BVP main page Boundary Value Problems

A directory/database of BVP problems.

PDE	BCs	ICs	Click for link to solution
1	2	3	4
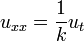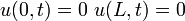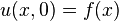$u_{xx}= \frac{1}{k} u_t$	$u(0,t)=0 \mbox{ } u(L,t)=0$	$u(x,0) = f(x)$	BVP_1D_heat_hom_dirichlet_hom
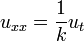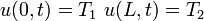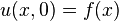$u_{xx}= \frac{1}{k} u_t$	$u(0,t)=T_1 \mbox{ } u(L,t)=T_2$	$u(x,0) = f(x)$	BVP_1D_heat_hom_dirichlet_non_hom
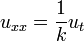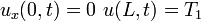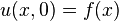$u_{xx}= \frac{1}{k} u_t$	$u_x(0,t)=0 \mbox{ } u(L,t)=T_1$	$u(x,0) = f(x)$	BVP_1D_heat_hom_neumann_dirichlet
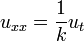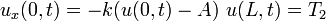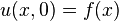$u_{xx}= \frac{1}{k} u_t$	$u_x(0,t)=-k(u(0,t)-A) \mbox{ } u(L,t)=T_2$	$u(x,0) = f(x)$	BVP_1D_heat_hom_dirichlet_non_hom
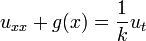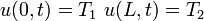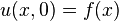$u_{xx} + g(x) = \frac{1}{k} u_t$	$u(0,t)=T_1 \mbox{ } u(L,t)=T_2$	$u(x,0) = f(x)$	BVP_1D_heat_hom_dirichlet_non_hom
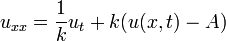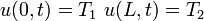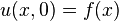$u_{xx}= \frac{1}{k} u_t + k(u(x,t)-A)$	$u(0,t)=T_1 \mbox{ } u(L,t)=T_2$	$u(x,0) = f(x)$	BVP_1D_heat_nonhom_dirichlet_non_hom
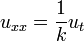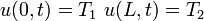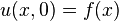$u_{xx}= \frac{1}{k} u_t$	$u(0,t)=T_1 \mbox{ } u(L,t)=T_2$	$u(x,0) = f(x)$	BVP_2D_Laplaces_hom_BCs_non_hom
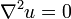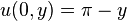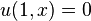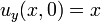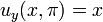$\displaystyle \nabla^2 u= 0$	$u(0,y)=\pi-y$ $u(1,x)=0$ $u_y(x,0) = x$ $u_y(x,\pi) = x$	none	click here to see pdf of Maple file that has solution.
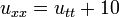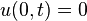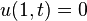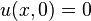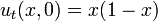$\displaystyle u_{xx} = u_{tt} + 10$	$u(0,t)=0$ $u(1,t)=0$	$u(x,0) = 0$ $u_t(x,0) = x(1-x)$	Click here to see pdf of a Maple file that has solution.
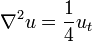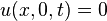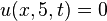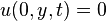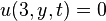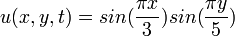$\displaystyle \nabla^2 u= \frac{1}{4}u_t$	$u(x,0,t)=0$ $u(x,5,t)=0$ $u(0,y,t) = 0$ $u(3,y,t) = 0$	$u(x,y,t)= sin(\frac{\pi x}{3}) sin(\frac{\pi y}{5})$	click here to see pdf of Maple file that has solution.
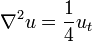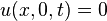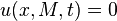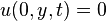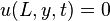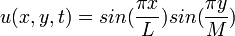$\displaystyle \nabla^2 u= \frac{1}{4}u_t$ + F(x,y,t)	$u(x,0,t)=0$ $u(x,M,t)=0$ $u(0,y,t) = 0$ $u(L,y,t) = 0$	$u(x,y,t)= sin(\frac{\pi x}{L}) sin(\frac{\pi y}{M})$
}

This article is issued from Wikiversity - version of the Tuesday, February 23, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.