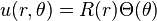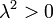Boundary Value Problems/Lesson 7

< Boundary Value Problems

Boundary Value Problems

Rectangular Domain (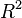R^2)

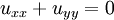
\displaystyle u_{xx} + u_{yy} = 0

Disk Domain (Polar)

Disc of radius c

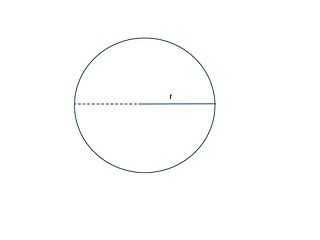
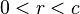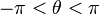
For a disk with a radius of "c", let the polar coordinates be 0 < r < c , and -\pi < \theta < \pi
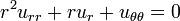
r^2 u_{rr} + r u_r + u_{\theta \theta}=0

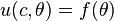u(c,\theta)=f(\theta) , boundary condition.

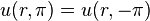u(r,\pi)=u(r,-\pi) continuity of potential.

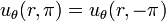u_{\theta}(r,\pi) = u_{\theta}(r,-\pi) continuity of derivative.

\displaystyle u(r,\theta) = R(r)\Theta(\theta)

The solution as a product of two independent functions. By substitution into the above PDE we have:

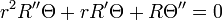
\displaystyle r^2 R'' \Theta + r R' \Theta + R \Theta '' =0

Separate,

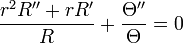
\displaystyle \frac {r^2 R'' + r R'}{R} + \frac {\Theta ''}{\Theta} =0
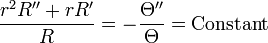
\displaystyle \frac {r^2 R'' + r R'}{R} = - \frac {\Theta ''}{\Theta}= \mbox {Constant}

The constant may be greater than , equal to or less than zero.


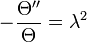
\displaystyle - \frac {\Theta ''}{\Theta}= \lambda^2

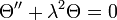
\displaystyle \Theta ''+ \lambda^2 \Theta= 0

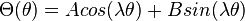
\displaystyle \Theta(\theta) = A cos(\lambda \theta) + B sin( \lambda \theta )
Use the continuity conditions and try to determine something more about A, B and λ.
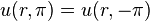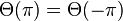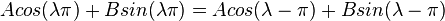
\displaystyle u(r,\pi)= u(r,-\pi) thus \displaystyle \Theta(\pi)= \Theta( -\pi) and \displaystyle A cos(\lambda \pi) + B sin( \lambda \pi )=A cos(\lambda -\pi) + B sin( \lambda -\pi )
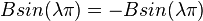
\displaystyle B sin( \lambda \pi )=- B sin( \lambda \pi )
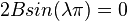
\displaystyle 2B sin( \lambda \pi )=0
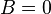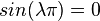
Either \displaystyle B=0 or \displaystyle sin( \lambda \pi )=0
Before choosing, apply the second boundary condition:

The continuity of the derivative provides a second condition:
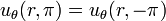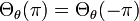
\displaystyle u_{\theta}(r,\pi)= u_{\theta}(r,-\pi) thus \displaystyle \Theta_{\theta}(\pi)= \Theta_{\theta}( -\pi)
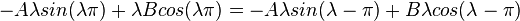
\displaystyle-A \lambda sin(\lambda \pi) + \lambda B cos( \lambda \pi )=-A \lambda sin(\lambda -\pi) + B \lambda cos( \lambda -\pi )
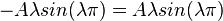
\displaystyle -A \lambda sin(\lambda \pi) =A \lambda sin(\lambda \pi)
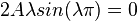
\displaystyle 2A \lambda sin(\lambda \pi) =0
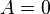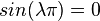
Either \displaystyle A=0 or \displaystyle sin( \lambda \pi) =0
If either A or B are zero then 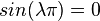\displaystyle sin( \lambda \pi) =0 also must hold. So all we need is 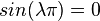\displaystyle sin( \lambda \pi) =0 which implies 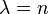\displaystyle \lambda = n . Remember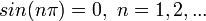 \displaystyle sin(n \pi) = 0, \mbox{ } n=1,2,...

Example of Potential equation on semi-annulus.

%%(php) <?php echo "Hello, World!"; ?> %%


Return to Main Page Boundary Value Problems

This article is issued from Wikiversity - version of the Saturday, August 30, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.