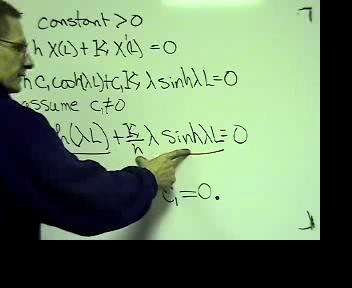Boundary Value Problems/Lesson 5.2
< Boundary Value ProblemsClick here to return to BVPs Boundary Value Problems
- Title: One 1D heat equation with several boundary conditions
- Objectives: Specifically what is to be retained by the learner.
- Setup of heat equation
- Solution of heat equation with homogeneous/nonhomogeneous Dirichlet, Neumann and mixed boudary conditions.
- Activities: Content directed at the learner to achieve learning objectives.
- Solve specific homework prooblems.
- Assessment: Determine lesson effectiveness in achieving the learning Objectives.
- Homework and quizzes
Background
The derivation of the Heat Equation
Heat Flow: Fourier's Law
What is heat? Heat is a form of energy that is measured in units of degree Celsius [1].
For a gas this measure is the average kinetic energy
of the molecules in the gas.
For a solid heat is associated with vibrational energy of the crystalline structure.
Heat is measured by us in units of degrees, these are related to calories by the definition, one calorie is the amount of heat required to increase the temperature of one gram of water(at one atmosphere of pressure) by one degree Celsius.
References
- ↑ a historical form of energy measurement is the calorie which is the amount of heat required to increase the temperature of one gram of water(at one atmosphere of pressure) by one degree Celsius.
How heat flows?
Let 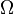 represent a region of space in
represent a region of space in 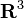 and
and 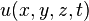 be the temperature at a point in
be the temperature at a point in 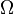 at a time
at a time 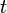 . From observation you know that heat flows from a high temperature region to a lower temperature region. Mathematically we represent this as
. From observation you know that heat flows from a high temperature region to a lower temperature region. Mathematically we represent this as  which is a vector pointing in the direction of decreasing temperatures. The negative gradient of
which is a vector pointing in the direction of decreasing temperatures. The negative gradient of 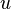 is a vector that points in the direction that the temperature is decreasing the most. Heat is flowing in that direction, at least locally.
is a vector that points in the direction that the temperature is decreasing the most. Heat is flowing in that direction, at least locally.
The heat flux vector 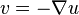 describes a vector field in
describes a vector field in 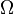 for the scalar field
for the scalar field 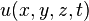 .
.
Think of 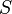 as a a surface in
as a a surface in 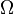 . As shown below.
. As shown below.
Fourier's Law
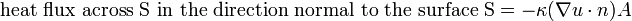
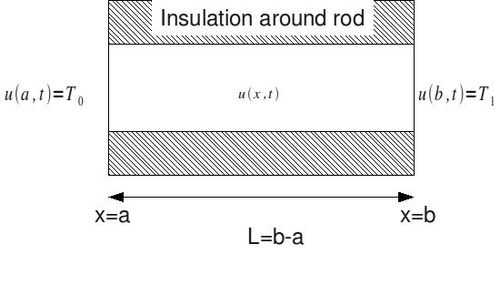
The temperature in a bar extending from  to
to 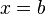 at a time
at a time 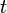 is
is 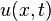 . The flow of heat in the bar leads to the development of the General Heat Equation in one spatial dimension. At this time I have not entered the material for this from my notes. It is found in a variety of standard BVP and DE textbooks. The derivation leads to the following PDE with boundary conditions and initial condition.
. The flow of heat in the bar leads to the development of the General Heat Equation in one spatial dimension. At this time I have not entered the material for this from my notes. It is found in a variety of standard BVP and DE textbooks. The derivation leads to the following PDE with boundary conditions and initial condition.
The general form for the heat equation in one spatial dimension is:
PDE 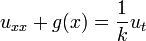 with the general boundary conditions
with the general boundary conditions
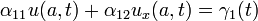
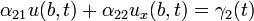
and the initial condition 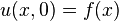 for
for 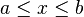 .
.
- Dirichlet Boundary Conditions: If
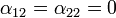 the problem is said to have Dirichlet boundary conditions.
the problem is said to have Dirichlet boundary conditions.
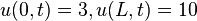 where
where 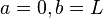 are Dirichlet BCs.
For this introductory work
are Dirichlet BCs.
For this introductory work 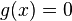 and
and 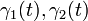 are constants.
are constants.
This will give us the simpler problem
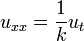 with the boundary conditions
with the boundary conditions
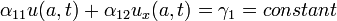
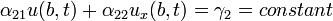
and the initial condition 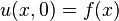 for
for 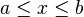 .
.
We first solve the problem with the BCs set to a fixed temperature of 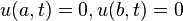 . The case is the result of setting
. The case is the result of setting 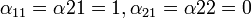 and
and 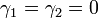
Homogeneous Boundary conditions for fixed end temperatures, Dirichlet
The rod is insulated along it's length and contains no sources or sinks is 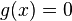 :
:
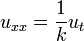

The general form for the accompanying boundary conditions at either end of the rod is:
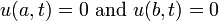 . Setting
. Setting 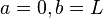 we have
we have 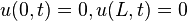 .
.
A quick knowledge check:
Lesson on Heat equation in 1D with Nonhomogeneous Dirichlet Boundary Conditions
Solve a nonhomogeneous Dirichlet BC problems.
and
.
- Setup the PDE and BCs
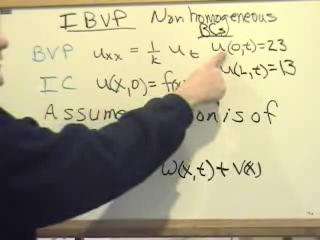
- Suppose the solution consists of a transitory component
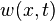 and a steady state component
and a steady state component 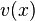 . To solve for
. To solve for 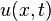 we will develop two problems. One will be assigned the nonhomogeneous BCs,
we will develop two problems. One will be assigned the nonhomogeneous BCs, 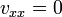 with nonzero end conditions
with nonzero end conditions 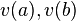 and the second problem will be assigned homogeneous BCs and the IC,
and the second problem will be assigned homogeneous BCs and the IC,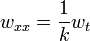 with zero end conditions
with zero end conditions 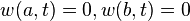 and
and 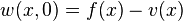 .
.
Solve for steady state part of the solution 
_v(x).ogv.jpg)
Just CLICK on the play button and the video will work , currently the thumnails for the uploads are messed up.

Neumann
The Neumann end condition is a first derivative condition on the heat flow across an end of the bar. The homogeneous case would have no heat flow, across a boundary
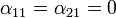 and
and 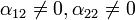 for all "t" and so
for all "t" and so
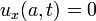 and
and 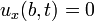 at the left and right boundaries when
at the left and right boundaries when 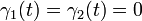 .
.
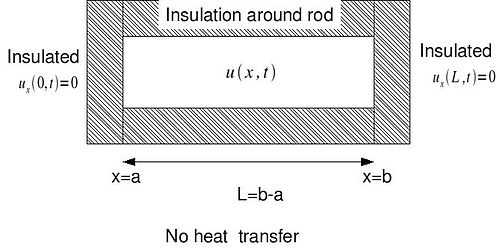
These are conditions where no heat flows across the ends of the rod. Thus no energy may enter or leave the rod.
Solution
Click on the PLAY arrow, video works. The thumbnails' jpeg images are the only thing messed up.

Mixed: Fixed Temp and Convection
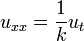 with the boundary conditions
with the boundary conditions
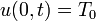 and
and
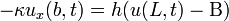
and the initial condition 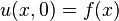 for
for 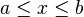 .
.
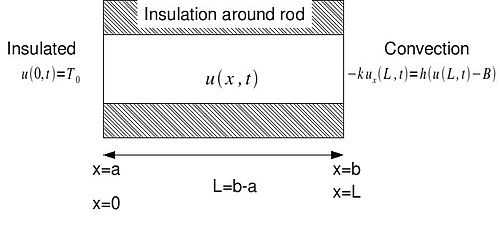
Lecture on setup of Heat equation for an insulated bar with one end held at a fixed temperature and the convective cooling applied to the second.

Lecture on solving for the steady steady 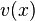 of Heat equation for an insulated bar with one end held at a fixed temperature and the convective cooling applied to the second.
of Heat equation for an insulated bar with one end held at a fixed temperature and the convective cooling applied to the second.

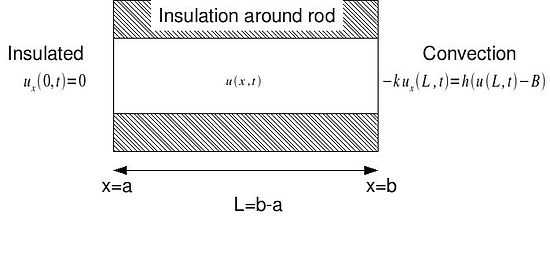
Heat 1d : Insulated and convective BCs
A bar of length L is insulated along it's length. One end is open to the air which is at 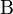 degrees and the other end is insulated so that there is no flow across the boundary.
degrees and the other end is insulated so that there is no flow across the boundary.
The heat equation is then:
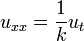 with the boundary condition s
with the boundary condition s
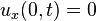 at the insulated end and
at the insulated end and 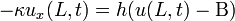 at the convective end.
at the convective end.
The intial temperature distribution is given by the function:
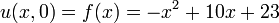
Just click on the Play button and video works!. The first video sets up the problem and starts the solution process.

The next video continues with the solution of the transient part of the problem.

This last video completes the transient solution and writes the series solution u(x,t).