Boundary Value Problems/Lesson 5.1
< Boundary Value ProblemsClick here to return to BVPs Boundary Value Problems
Lesson Plan
Requirements of student preparation: The student needs to have worked with vectors. If not the student should obtain suitable instruction in vector calculus.
- Subject Area: A review of vectors, vector operations, the gradient, scalar fields ,vector fields, curl, and divergence.
- Objectives: The learner needs to understand the conceptual and procedural knowledge associated with each of the following
- Vectors,
- Definition of vectors in
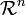 for
for 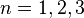
- Vector Operations
- Definition of vectors in
- Scalar and vector fields
- Gradient
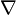 , divergence
, divergence 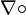 , curl
, curl 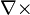 and covariant derivatives on fields
and covariant derivatives on fields - Composite operators such as
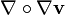
- Vectors,
- Activities: These structures are to help you understand and aid long-term retention of the material.
- Lesson on Vectors, their associated properties and operations that use vectors.
- Lesson on Scalar and Vector fields
- Lesson on Operations on scalar and vector fields
- Assessment: These items are to determine the effectiveness of the learning activities in achieving the lesson objectives.
- Worksheets
- Quizzes
- Challenging extended problems.
- Student survey/feedback
- Web analytics
Lesson on Vectors
We will be using only real numbers in this course. The set of all real numbers will be represented by 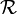 .
.
Definition of a scalar:
A scalar is a single real number, 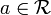 . For example
. For example 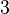 is a scalar.
is a scalar.
Definition of a real vector:
A real vector, 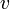 is an ordered set of two or more real numbers.
is an ordered set of two or more real numbers.
For example: 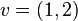 ,
, 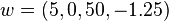 are both vectors. We will use the notation of
are both vectors. We will use the notation of 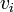 where the lower index
where the lower index 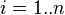 represents the individual elements of a vector in the appropropriate order.
represents the individual elements of a vector in the appropropriate order.
Ex: The vector 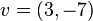 has two elements, the first element is designated
has two elements, the first element is designated 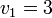 and the second is
and the second is 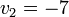
Dimension of a vector:
The dimension of a vector is the number of elements in the vector.
Ex: Dimension of 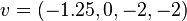 is
is 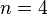
Vector Operations:
To refresh your memory, for vectors of the same dimension the following are valid operations:
Let 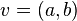 and
and 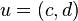 for each of the following statements.
for each of the following statements.
- Addition:
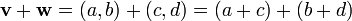
Ex: 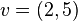 and
and 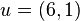 then
then 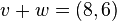
- Multiplication by a scalar,
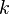 :
: 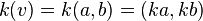
Ex:  and
and 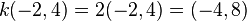
- Cross Product
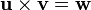
Let 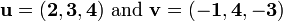 then
then
![\bold{u} \times \bold{v} =\left [ \begin{array}{ccc} i&j&k\\ 2&3&4
\\ -1&4&-3
\end{array} \right ] = \bold{i}(3 (-3)- 4^2) - \bold{j} (2 (-3) -4 (-1)) + \bold{k} (2(4)- 3(-1)](../I/m/8b960f77f0ac68ee798b5b2b730adbb5.png)
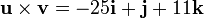
Lesson on Scalar and Vector Fields
Lesson on Solving Boundary Value Problems with Nonhomogeneous BCs
- Watch
 .
.