Boundary Value Problems/Lesson 4.1

Return to previous page Boundary_Value_Problems

Sturm Liouville and Orthogonal Functions

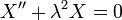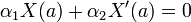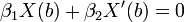The solutions in this BVP course will ALL be expressed as series built on orthogonal functions. Understanding that the simple problem $X'' + {\lambda}^2 X = 0$ with the boundary conditions $\alpha_1 X(a) + \alpha_2 X'(a) =0$ and $\beta_1 X(b) + \beta_2 X'(b) =0$ leads to solutions 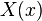$X(x)$ that are orthogonal functions is crucial. Once this concept is grasped the majority of the work in this course is repetitive.
In the following notes think of the function 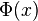$\Phi (x)$ as a substitution for $X(x)$ .

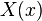TO SEE ALL OF THE PAGES DOUBLE CLICK ON THE FIRST PAGE. THEN YOU WILL BE ABLE TO DOWNLOAD NOTES. THESE WILL BE CONVERTED FOR THE WIKI AALD (at a later date)

Fourier Series

From the above work, solving the problem:
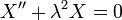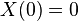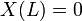$X'' + {\lambda}^2 X = 0$ with the boundary conditions $X(0) =0$ and $X(L) =0$ leads to an infinite number of solutions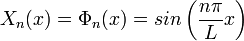 $X_n(x)= \Phi_n(x) = sin \left ( \frac{n \pi}{L} x \right )$
. These are eigenfunctions with eigenvalues 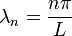$\lambda_n = \frac{n \pi}{L}$

Homework Assignment from Powell's sixth edition Boundary Value Problems page 71.

Project 1.2

This is a fourier series application problem.
You are given the piecewise defined function 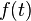$f(t)$ shown in the following graph.

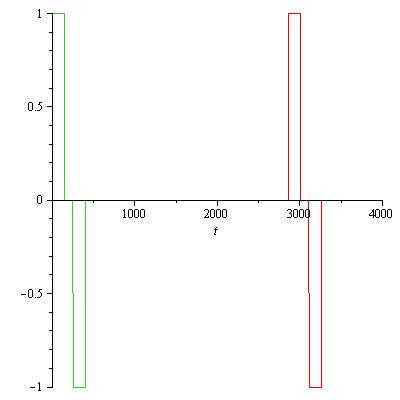
The positive unit pulse is 150 μs in duration and is followed by a 100 μs interval where f(t) =0. Then f(t) is a negative unit pulse for 150 μs once again returning to zero. This pattern is repeated every 2860 μs. We will attempt to represent f(t) as a Fourier series,

Determine the value of the period: Ans. Period is 2860 μs. The time for a complete repetition of the waveform.
Find the Fourier Series representation: 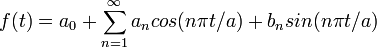$f(t) = a_0 + \sum_{n=1}^{\infty} a_n cos(n \pi t / a ) + b_n sin(n \pi t / a)$ .The video provides an explanation of the determining the coefficients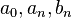 $a_0,a_n , b_n$

This is the first image.

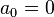
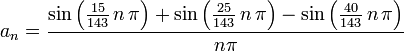
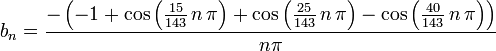
. The results are: $a_0 = 0$ $a_n = \frac {\sin \left( {\frac {15}{143}}\,n\,\pi \right) +\sin \left( {\frac {25}{143}}\,n\,\pi \right) -\sin \left( {\frac {40}{143}}\,n\,\pi \right) } {n \pi }$ $b_n= \frac {- \left( -1+\cos \left( {\frac {15}{143}}\,n\,\pi \right) +\cos \left( {\frac {25}{143}}\,n\,\pi \right) -\cos \left( {\frac {40}{ 143}}\,n\,\pi \right) \right)} {n \pi}$

Using 100 terms an approximation is;
Shift 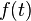$f(t)$ right or left by an amount 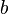$b$ such that the resulting periodic function is an odd function. Here is a plot of shifting it to the left half way between the +1 and -1 pulses. This is a shiift of b= 200 μs. The new funnction is 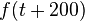$f(t+200)$ . A plot follows: 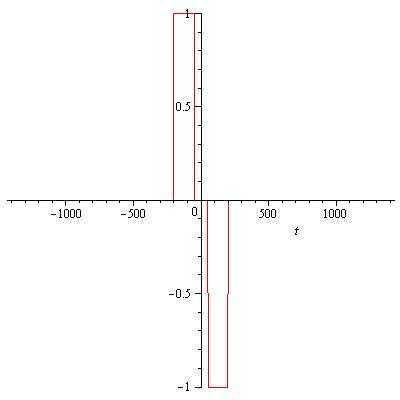. It could also be shifted to the right by 1230 μs, that is 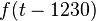$f(t-1230)$ is the new function.

This article is issued from Wikiversity - version of the Tuesday, February 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.