Boundary Value Problems/Introduction

An example of a boundary value problem in one dimension is the second order linear differential equation:

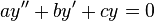$ay'' + by' + cy = 0$ with the end conditions of 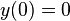$y(0)=0$ and $y(L) =0$ .

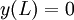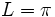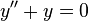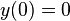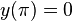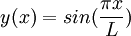For a simple problem let a=1, b=0, c=1 and $L = \pi$ . The resulting differential equation is $y''+ y = 0$ with boundary conditions $y(0)=0$ and $y(\pi) =0$ . A solution is $y(x) = sin ({{\pi x} \over L})$ .

A plot of this solution is shown below. Note that the solution satisfies the boundary conditions.

For more information about ordinary differential equations and methods for solving them, use the following link ODE

This article is issued from Wikiversity - version of the Tuesday, February 23, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.