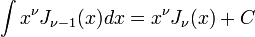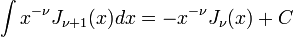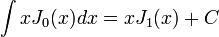Bessel functions
| | Resource type: this resource contains a lecture or lecture notes. |
Definition
The Bessel function is canonical solution to Bessel's differential equation 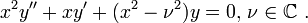 Solutions were first introduced by Daniel Bernoulli, but later generalized by Friedrich Bessel. The most common and most important case of the Bessel function is when
Solutions were first introduced by Daniel Bernoulli, but later generalized by Friedrich Bessel. The most common and most important case of the Bessel function is when 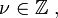 which is called the order of the Bessel function.
which is called the order of the Bessel function.
Bessel functions arise when the method of separation of variables is applied to the Laplace or Helmholtz equation in cylindrical or spherical coordinates. They are very important for many problems dealing with physical phenomena, like wave or heat propagation.
Derivation of Bessel function using Frobenius's Method
Consider the Bessel equation:
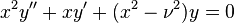
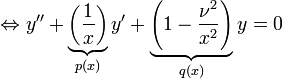
We're seeking solutions near 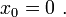 Since:
Since:
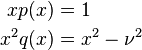
are power series in x, 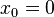 is a regular singular point of the Bessel equation. This allows Frobenius's method to be applied.
is a regular singular point of the Bessel equation. This allows Frobenius's method to be applied.
We are seeking solutions of the form:
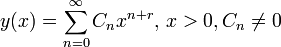
Differentiating yields:
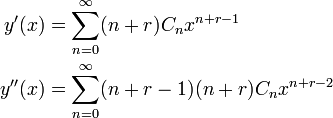
Conditions for  must be found. Substituting our expressions back into the Bessel equation:
must be found. Substituting our expressions back into the Bessel equation:
A substitution must be made in indices: This yields:
This yields:
![\begin{align}
0 & =\sum_{n=0}^\infty \left [ (n+r-1)(n+r)+(n+r)-\nu^2 \right ] C_nx^{n+r} + \sum_{m=2}^\infty C_{m-2}x^{m+r} \\
& =\sum_{n=0}^\infty \left [ (n+r)^2-\nu^2 \right ] C_nx^{n+r} + \sum_{n=2}^\infty C_{n-2}x^{n+r} \\
& =(r^2-\nu^2)C_0x^r+ [(r+1)^2-\nu^2]C_1x^{r+1}+\sum_{n=2}^\infty \left \{ [(n+r)^2-\nu^2]C_n+C_{n-2} \right \} x^{n+r}
\end{align}](../I/m/bd4736898e804e1c4aa311d8c917eeb8.png)
Dividing the equation above by  yields:
yields:
![0 =(r^2-\nu^2)C_0+ [(r+1)^2-\nu^2]C_1x+\sum_{n=2}^\infty \left \{ [(n+r)^2-\nu^2]C_n+C_{n-2} \right \} x^n](../I/m/29d111b1d93e4fe48b92f6a41e484345.png)
By the "Identity Theorem" (which states that xn is linearly independent), it follows that:
![\begin{align}
& (r^2-\nu^2)C_0 = 0 \\
& [(r+1)^2-\nu^2]C_1=0 \\
& [(n+r)^2-\nu^2]C_n+C_{n-2}=0, \, n=2,3,4,\cdots
\end{align}](../I/m/b7e375ea6a1b9a1320cc18117ff9d869.png)
By assumption, 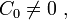 so we define a function:
so we define a function:
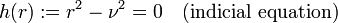
The possible values for 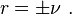 Let
Let 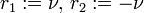 and for convenience, let
and for convenience, let 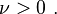 We obtain the following recurrence relations for
We obtain the following recurrence relations for 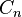 :
:
![\begin{cases}
C_0 \neq 0 \quad \text{(arbitrarily defined)} \\
C_1 = 0 \quad \text{(follows from } [(r+1)^2-\nu^2]C_1=0 \text{)} \\
\underbrace{[(n+r)^2-\nu^2]}_{h(n+r)}C_n=-C_{n-2}, \, n=2,3,4,\cdots
\end{cases}](../I/m/4db1e7f6fd9d94be779e22de11ea910b.png)
To get a solution to the Bessel equation, choose 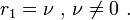 Thus,
Thus, 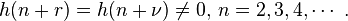 We can now solve for
We can now solve for 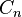 :
:
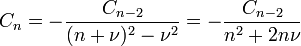
We end up with the recursion:
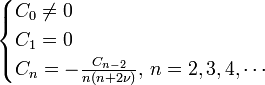
Since the recursion has depth 2 and 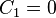 , it follows that:
, it follows that:
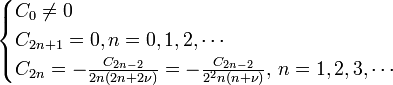
Because of the recursion, we get the following set of terms:
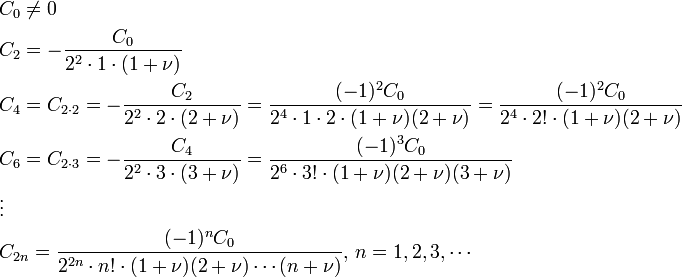
In order to simplify the expansion of y, we normalize 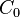 and choose:
and choose:
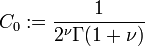
This simplifies our general term to:
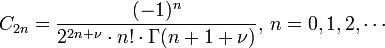
The first solution to the Bessel equation can be written like this:
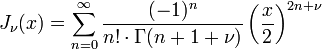
Gamma Function
Definition
The definition of the gamma function is defined on 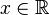 such that
such that 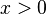 :
:
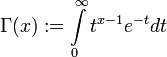
Properties of the Gamma Function
Here are some theorems for the gamma function:
Second Solution of the Bessel Equation
For the case that 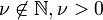 , we can define a second solution to the Bessel function. In this case,
, we can define a second solution to the Bessel function. In this case, 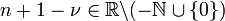 and therefore
and therefore 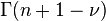 is defined. Consider:
is defined. Consider:
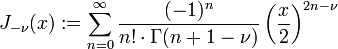
Some theorems for this new function:
-
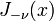 solves the Bessel equation.
solves the Bessel equation. -
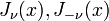 are linearly independent.
are linearly independent.
These theorems are proved easily, but will not be shown here.
Bessel Functions of the Second Kind
A second function that is defined on 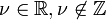 takes the form:
takes the form:
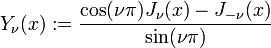
Deriving this result is fairly difficult and will not be shown here. This function, called the Bessel function of the second kind of order 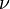 , is linearly independent from
, is linearly independent from 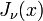 .
.
Hankel Functions, Bessel Functions of the Third Kind
A third type of function (complex-valued) for 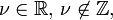 are:
are:
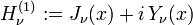
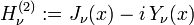
and are called the Bessel functions of the 3rd kind or Hankel functions of order 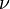 . The Hankel functions
. The Hankel functions 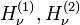 are linearly independent.
are linearly independent.
Complete Solution to the Bessel Equation
For all 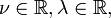 the complete solution of the Bessel equation:
the complete solution of the Bessel equation:
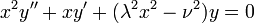
can be written as:
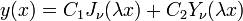
or:
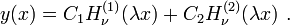
If 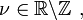 then:
then:
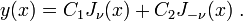
Moreover:
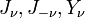 have countably many zeroes.
have countably many zeroes.- If
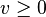 , then
, then 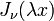 is finite for all
is finite for all 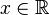 ,
, 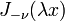 and
and 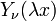 are unbounded in the neighborhood of 0.
are unbounded in the neighborhood of 0.
Identities
Here are some identities for the Bessel function. They can be deduced with reasonable effort.
Differential Identities
For 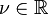 :
:
Corollary:
Corollary (Recursion Formula):
Integration Identities
For 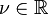 :
:
Important special cases 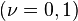 :
:
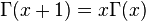
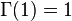
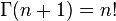
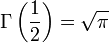
![\left [ x^{\nu} J_{\nu}(x)\right ]' = x^{\nu} J_{\nu-1}(x)](../I/m/ebed04a88538b18a2b862e8f2fd53ce4.png)
![\left [ x^{-\nu} J_{\nu}(x)\right ]' = -x^{-\nu} J_{\nu+1}(x)](../I/m/259c3ebb49b6b60d4c139a8c14dc533c.png)
![\left [ x^{\nu} Y_{\nu}(x)\right ]' = x^{\nu} Y_{\nu-1}(x)](../I/m/50cc0e6f7814e3e5c81e784826864431.png)
![\left [ x^{-\nu} Y_{\nu}(x)\right ]' = -x^{-\nu} Y_{\nu+1}(x)](../I/m/ca47d296b21447855066371d1d487b09.png)
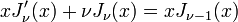
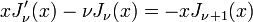
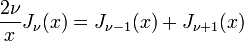
![J_\nu'(x)=\frac{1}{2} \left [ J_{\nu-1}(x) - J_{\nu+1}(x) \right ]](../I/m/5c419d251206a2715ddf9e260ee804eb.png)