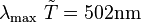Astronomy college course/Introduction to stellar measurements/questions/answers

< Astronomy college course < Introduction to stellar measurements < questions

Stellar Parallax (#1)

Stellar parallax is an annual change in angular position of a star as seen from Earth. (Annual means it happens every year; the change occurs because of Earth's rotation about the Sun.)

Luminosity (#2)

Luminosity is the total amount of energy emitted per unit time. In other words, it is the amount of energy divided by the time over which this energy is measured, otherwise known as "power".

Standard candle (#3)

A standard candle is an astronomical object with known luminosity (useful for calculating the distance via d=b/θ)

Absolute magnitude (#4)

Absolute magnitude is a numerical measure of brightness as seen from a distance of approximately 32.6 light-years. More precisely, it is the relative magnitude that object would have if it were exactly one parsec from us.

Relative magnitude (#5)

Relative magnitude is a numerical measure of brightness as seen from Earth. We use the phrase "numerical measure" because the relationship between magnitude and luminosity is rather messy to do algebraically (involves logarithms, not really to base 10 but more like to base 2.512).

Maximum distance for using parallax (#6)

In 1989 the satellite Hipparcos was launched primarily for obtaining parallaxes and proper motions allowing measurements of stellar parallax for stars up to about 500 parsecs away, which is about 0.015 times the diameter of the Milky Way Galaxy.} + .015

Peak (maximum) wavelength and temperature (#7)

An object emits thermal (blackbody) radiation with a peak wavelength of 250nm. How does its temperature compare with the Sun?

Answer: Wein's law relates the peak emission wavelength, λ_max, to temperature. If temperature is measured in units of the Sun's temperature, 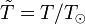$\tilde T = T/T_\odot$ , where 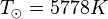$T_\odot=5778K$ is the surface temperature of the Sun. In these units, Wein's law can be written:

$\lambda_\text{max} \ \tilde T = 502\text{nm}$

Peak wavelength, λ_max, is measured in nanometers (1nm=10^-9m). This implies that the maximum wavelength of the Sun is about 500 nm (since $\tilde T = 1$ for the Sun).

In our problem, the wavelength is cut in half. That will happen if the star's temperature doubles, i.e., if 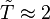$\tilde T \approx 2$ :

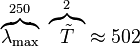
$\overbrace{\lambda_\text{max}}^{250} \ \overbrace{\tilde T}^2 \approx 502$

The star is 2 times hotter than the Sun

Normalized intensity (measure of relative magnitude) versus distance and luminosity (#8)

The "normalized intensity" of a Sun-like star situated one parsec from Earth would be 4πI = 1. What is 4πI for a star with 100 times the Sun's energy output that is situated 10pc from Earth?

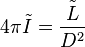$4\pi \tilde I=\frac{\tilde L}{D^2}$ is a "normalized intensity", closely related to relative magnitude, that allows students to combine equations and solve problems without resorting to the logarithmic magnitude scale. If the distance to the stellar object, D, is measured in parsecs, it is the power per square parsec that enters a telescope on Earth.

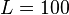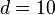Answer: In our case $L=100$ and $d=10$ in the units we are using.

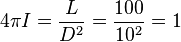4\pi I=\frac{L}{D^2}=\frac{100}{10^2}=1

normalized units of the star's intensity as seen from Earth.

Since it equals 1 in this case, the star appears exactly as bright as the Sun would if the sun were 1 parsec away.

Look at it this way: Consider a star exactly as luminous as the Sun that is situated at a distance of one parsec. Now make it 100 times brighter and 10 times further away. This calculation indicates that it would not change as seen from Earth.

Parallax using an orbiting satellite (which has never been built): (#9)

An orbiting satellite makes a circular orbit 5 AU from the Sun. It measures a parallax angle of 0.2 of an arcsecond (each way from the average position). What is the star's distance?

Answer:

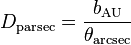$D_\mathrm{parsec}=\frac{b_\mathrm{AU}}{\theta_\mathrm{arcsec}}$ , where D is the distance to the object in parsecs, θ is the parallax angle in arcseconds, and b is the baseline in AU; b=1 for observations taken from Earth. One degree is 60 arcminutes and one arcminute is 60 arseconds. One AU ≈ 1.5x10¹¹ meters, and one parsec ≈ 3.26 light-years, and one light-year ≈ 9.5×10¹⁵ meters.

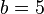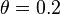In our case, $b=5$ and $\theta = 0.2$ in the units we are using.

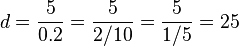d = \frac{5}{0.2}=\frac{5}{2/10}=\frac{5}{1/5}=25

(parsecs)

Luminosity, size, and temperature (#10)

A star that is increasing it's temperature while maintaining constant luminosity is Answer: 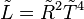$\tilde L=\tilde R^2\tilde T^4$ , where 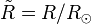$\tilde R=R/R_\odot$ is the radius and temperature normalized to the Sun's radius and 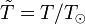$\tilde T=T/T_\odot$ is the temperature normalized to the Sun's temperature. Since 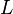$L$ is constant, we see that radius, or 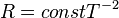$R = const T^{-2}$ is inversely proportional to the square of the temperature. If one goes up the other goes down. Since temperature is increasing, we conclude that the star is

getting smaller in size

Wavelengths of visible light (#11)

The range of wavelength for visible light is between 400 and 700 nanometers (as can be read off the electromagnetic spectrum chart)

Reading the "contours" of constant R on the HR diagram (#12)

Based on the HR diagrams and images in stars shown in the materials, a very large red supergiant has a diameter that is about 3x10⁵ greater than a small white dwarf. The diagonal lines in the HR diagram represent lines along which the radius remains constant. If one goes from the absolute outer edge of both regions, one obtains 10⁶, which is about 3 times larger than the answer given. But it is 30 times smaller than the next largest possible answer, which is 3x10⁷

This article is issued from Wikiversity - version of the Monday, April 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.