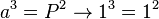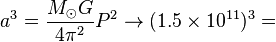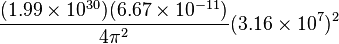Astronomy college course/Introduction to stellar measurements

A few definitions

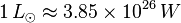Luminosity: In astronomy, luminosity is total amount of energy emitted by a star or other astronomical object per unit time. In SI units this is expressed as joules per second or watts. I.e. The Sun has a total power output of 3.846×10²⁶ Watts (that's a lot of light bulbs!). A more convenient unit of luminosity is this Sun itself: 1.00 solar luminosity, or $1\,L_\odot\approx3.85\times10^{26}\,W\,$ .
Relative magnitude: a numerical measure of an astronomical object as seen from Earth; a decrease of 1 unit represents an increase in the light received by a factor of 2.512. In other words, the larger the relative magnitude, the fainter the object appears to be.^[1]
Absolute magnitude: a numerical measure of an astronomical object as seen from a distance of 10 parsecs or 32.6 light years. An object's relative and absolute magnitudes are equal if and only if teh object is 10 parsecs from Earth (neglecting extinction effects). As with relative magnitude words, the larger the absolute magnitude, the less luminous the object actually is.^[2]

(Malaysian)

Stellar parallax: The change of angular position of a star as seen from Earth, due to the motion of the Earth around the Sun. The star's angular shift that occurs when the observer moves by AU (one astronomical unit) In 1989 the satellite Hipparcos was launched primarily for obtaining parallaxes and proper motnios allowing measurements of stellar parallax for stars up to about 500 parsecs away, a little more than one percent of the diameter of the Milky Way Galaxy.^[3]
Standard candle: an astronomical object that has a known luminosity.

A perplexing array of standard candles. The fainter and more common nearby candles are used to calibrate the ultra-Luminous and exotic objects that allow us to measure distances reaching billions of light years away.

The figure to the left shows what Wikipedia calls the w:Cosmic distance ladder.^[4] The ladder analogy arises because no one technique can measure distances at all ranges encountered in astronomy. Instead, one method can be used to measure nearby distances, a second can be used to measure nearby to intermediate distances, and so on. Each rung of the ladder provides information that can be used to determine the distances at the next higher rung.

Equations

Angular size, size, and distance

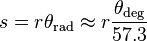$s=r\theta_\mathrm{rad}\approx r\frac{\theta_\mathrm{deg}}{57.3}\,$ is the arclength of a portion of a circle of radius r described the angle θ. The two forms allow θ to be measured in either degrees or radians (2π rad = 360 deg). The lengths r and s must be measured in the same units.

Using your hand to measure angules

Stellar parallax

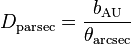$D_\mathrm{parsec}=\frac{b_\mathrm{AU}}{\theta_\mathrm{arcsec}}$ , where D is the distance to the object in parsecs, θ is the parallax angle in arcseconds, and b is the baseline in AU; b=1 for observations taken from Earth. One degree is 60 arcminutes and one arcminute is 60 arseconds. One AU ≈ 1.5x10¹¹ meters, and one parsec ≈ 3.26 light-years, and one light-year ≈ 9.5×10¹⁵ meters.

Newton's version of Kepler's third law

Kepler (1571-1630) found a relation between period and average distance for all planets and comets around the Sun. Newton (1643-1727) discovered "universal" laws which not only explained Kepler's third law, but showed that the applied on earth, around other planets, as well as for stars and clusters of stars. His addition of the "total mass" allows us to "weigh" (technically "mass" almost anything and everything in the universe.

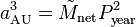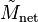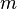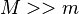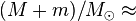
$a_\mathrm{AU}^3=\tilde M_\mathrm{net}P_\mathrm{year}^2$ , where P is the period of orbit in years, and a is the semi-major axis measured in AU. The net mass, $\tilde M_\mathrm{net}$ , is the sum of the mass of both bodies, and is normalized to the mass of the Sun. For a planet of mass, $m$ , orbiting a star of of much larger mass, $M>>m$ , the normalized net mass is 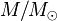$\tilde M_\mathrm{net}=\,$ $(M+m)/M_\odot\approx\,$ $M/M_\odot$ . The mass of the Sun, 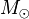$M_\odot$ , is 1.99×10³⁰ kilograms. If 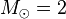$M_\odot =2$ for some object, then that object is twice as massive as the Sun. One year is 3.15×10⁷ seconds.

Normalized units

Kepler's third law is a relation between the period of a planet and an averaged distance (semi-major axis) from the Sun. It takes on a simple form if the period is measured in years and the distance is measured in AU. For Earth, we have:

a^3=P^2\rightarrow 1^3=1^2\;

In contrast, if time is measured in seconds and distance in meters, then the Kepler's third law for Earth looks like this:

a^3= \frac{M_\odot G}{4\pi^2}P^2\rightarrow (1.5\times 10^{11})^3=

\frac{(1.99\times 10^{30})(6.67\times 10^{-11})}{4\pi^2}(3.16\times 10^{7})^2

In the previous section, the Kepler/Newton relation between mass, period and semi-major axis are most conveniently written using the following units:

Time is measured in years
Distance is measured in AU
Mass is measured in solar masses.

In the next sections, we find it helpful to define:

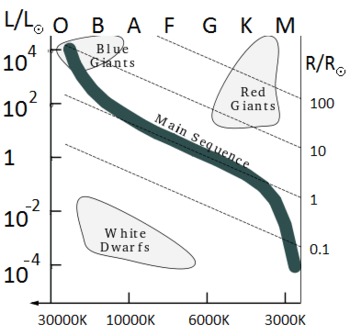
Power (L) is measured in units of the Sun's power output
Temperature (T) is measured in units of the Sun's temperature.
Radius (R) is measured in units of the Sun's radius.

To remind the reader that these normalized, a tilde shall be placed over the variables. If a star's temperature is expressed as 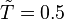$\tilde T = 0.5$ and its radius is 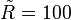$\tilde R = 100$ , then its surface is half that of the Sun, and it is 100 times larger than the Sun.

Two facts about how blackbodies "glow"

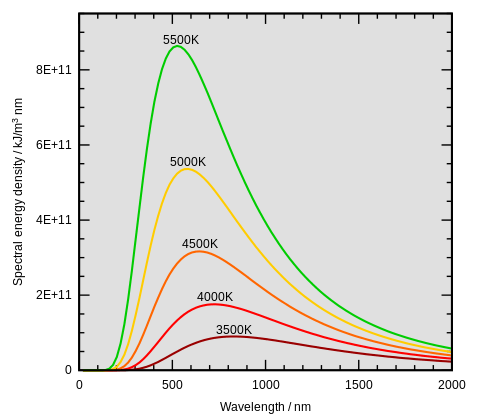
A hot object gives off electromagnetic radiation. We sometimes experience this as visible light given off by every hot objects, or as heat given off by a campfire. While these phenomena have been observed for centuries, a mathematical understanding only emerged only by the first decade of the 20th century with the revolutionary idea that light was both a particle ('photon') and a wave. The following formulas are strictly true only for a blackbody, but they are good approximations for stars, since most photons that strike a star get 'lost' in the star. The color of a black body is closely related to it's temperature. Here 'color' refers to the peak wavelength emitted by the star:

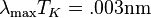$\lambda_\text{max} T_K = .003\text{nm}$ is Wein's law that relates the peak emission wavelength, λ_max, of a black body to temperature, T measured in Kelvins. Peak wavelength, λ_max, is measured in nanometers (1nm=10^-9m). If temperature is measured in units normalized to the Sun's temperature, 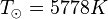$T_\odot=5778K$ , then
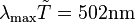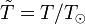$\lambda_\text{max} \tilde T = 502\text{nm}$ where $\tilde T=T/T_\odot$ is the temperature normalized to the Sun's temperature.

The Stefan-Boltzmann law is usually written as P=σAT⁴, where A is surface area, T is temperature (in Kelvins), and σ is the Stefan-Boltzmann constant. The power, P, can be written as normalized luminosity, 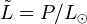$\tilde L = P/L_\odot$ , where L_☉ =3.85×10²⁶W is the power output (or luminosity) of the Sun. In these normalized units, the Stefan-Boltzmann law is:

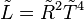$\tilde L=\tilde R^2\tilde T^4$ , where 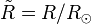$\tilde R=R/R_\odot$ is the radius and temperature normalized to the Sun's radius and 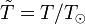$\tilde T=T/T_\odot$ is the temperature normalized to the Sun's temperature.

The Stefan-Boltzmann constant, σ, is a fundamental constant (like Newton's G, Planck's h, or even Einstein's c).

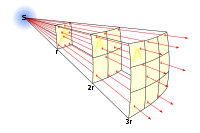
Inverse square law

Relative magnitude is a common measure of how bright an object appears to be from Earth. Unfortunately this is a Logarithmic scale that renders calculations somewhat advanced. Instead we shall use intensity, normalized to units where power is measured in units of Solar luminosity:

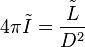$4\pi \tilde I=\frac{\tilde L}{D^2}$ is a "normalized intensity", closely related to relative magnitude, that allows students to combine equations and solve problems without resorting to the logarithmic magnitude scale. If the distance to the stellar object, D, is measured in parsecs, it is the power per square parsec that enters a telescope on Earth. The luminosity, 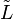$\tilde L$ , (in solar units) is a measure of the absolute magnitude. In general, 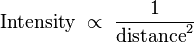$\mbox{Intensity} \ \propto \ \frac{1}{\mbox{distance}^2} \,$ is the inverse-square law.

For example, I=1/4π for a star like the Sun situated one parsec away, provided intensity is measured as Solar luminosities per square parsec. To see how much energy (or power) enters a telescope, it is necessary to calculate the area of the telescope in square parsecs.

click to see the references

(Many are from Wiktionary)

↑ https://en.wiktionary.org/w/index.php?title=apparent_magnitude&oldid=23450540
↑ https://en.wiktionary.org/w/index.php?title=absolute_magnitude&oldid=24168207
↑ https://en.wikipedia.org/w/index.php?title=Stellar_parallax&oldid=586855433
↑ https://en.wikip edia.org/w/index.php?title=Cosmic_distance_ladder&oldid=600781949

This article is issued from Wikiversity - version of the Thursday, June 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.