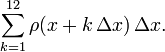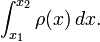Applying definite integrals
For a discussion on the basic theory of integrals see: w:Riemann sum
Imagine an object  that is free to move in one dimension — say, along the
that is free to move in one dimension — say, along the  axis. Like every physical object, it has a more or less fuzzy position (relative to whatever reference object we choose). For the purpose of describing its fuzzy position, quantum mechanics provides us with a probability density
axis. Like every physical object, it has a more or less fuzzy position (relative to whatever reference object we choose). For the purpose of describing its fuzzy position, quantum mechanics provides us with a probability density 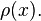 This depends on actual measurement outcomes, and it allows us to calculate the probability of finding the particle in any given interval of the
This depends on actual measurement outcomes, and it allows us to calculate the probability of finding the particle in any given interval of the  axis, provided that an appropriate measurement is made.
axis, provided that an appropriate measurement is made.
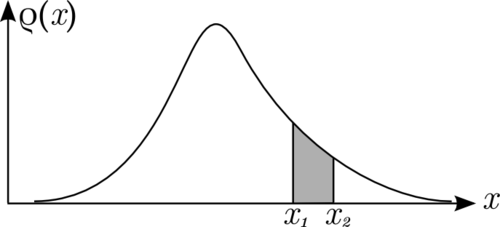
We call 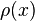 a probability density because it represents a probability per unit length. The probability of finding
a probability density because it represents a probability per unit length. The probability of finding 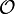 in the interval between
in the interval between  and
and 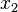 is given by the area
is given by the area 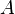 between the graph of
between the graph of 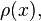 the
the  axis, and the vertical lines at
axis, and the vertical lines at  and
and 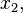 respectively.
How do we calculate this area? The trick is to cover it with narrow rectangles of width
respectively.
How do we calculate this area? The trick is to cover it with narrow rectangles of width 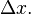
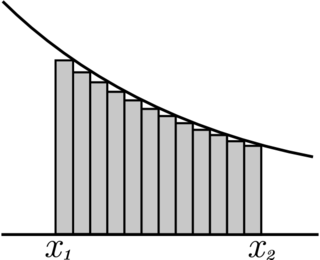
The area of the first rectangle from the left is 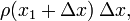 the area of the second is
the area of the second is 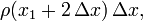 and the area of the last is
and the area of the last is 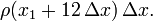 For the sum of these areas we have the shorthand notation
For the sum of these areas we have the shorthand notation
It is not hard to visualize that if we increase the number 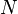 of rectangles and at the same time decrease the width
of rectangles and at the same time decrease the width 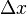 of each rectangle, then the sum of the areas of all rectangles fitting under the graph of
of each rectangle, then the sum of the areas of all rectangles fitting under the graph of 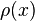 between
between  and
and 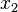 gives us a better and better approximation to the area
gives us a better and better approximation to the area 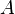 and thus to the probability of finding
and thus to the probability of finding 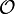 in the interval between
in the interval between  and
and 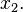 As
As 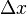 tends toward 0 and
tends toward 0 and 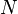 tends toward infinity (
tends toward infinity (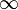 ), the above sum tends toward the integral
), the above sum tends toward the integral
We sometimes call this a definite integral to emphasize that it's just a number. (As you can guess, there are also indefinite integrals, about which more later.) The uppercase delta has turned into a 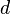 indicating that
indicating that 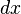 is an infinitely small (or infinitesimal) width, and the summation symbol (the uppercase sigma) has turned into an elongated S indicating that we are adding infinitely many infinitesimal areas.
is an infinitely small (or infinitesimal) width, and the summation symbol (the uppercase sigma) has turned into an elongated S indicating that we are adding infinitely many infinitesimal areas.
Don't let the term "infinitesimal" scare you. An infinitesimal quantity means nothing by itself. It is the combination of the integration symbol 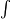 with the infinitesimal quantity
with the infinitesimal quantity 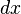 that makes sense as a limit, in which
that makes sense as a limit, in which 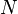 grows above any number however large,
grows above any number however large, 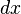 (and hence the area of each rectangle) shrinks below any (positive) number however small, while the sum of the areas tends toward a well-defined, finite number.
(and hence the area of each rectangle) shrinks below any (positive) number however small, while the sum of the areas tends toward a well-defined, finite number.