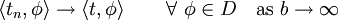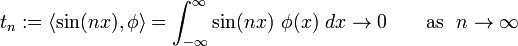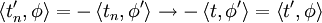Applied linear operators and spectral methods/Weak convergence
< Applied linear operators and spectral methodsConvergence of distributions
Definition:
A sequence of distributions  is said to converge to the distribution
is said to converge to the distribution
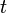 if their actions converge in
if their actions converge in 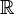 , i.e.,
, i.e.,
This is called convergence in the sense of distributions or weak convergence.
For example,
Therefore, 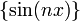 converges to
converges to 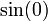 as
as 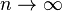 , in
the weak sense of distributions.
, in
the weak sense of distributions.
If 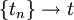 if follows that the derivatives
if follows that the derivatives 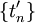 will
converge to
will
converge to 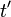 since
since
For example, 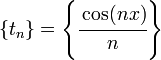 is both a
sequence of functions and a sequence of distributions which, as
is both a
sequence of functions and a sequence of distributions which, as
 , converge to 0 both as a function (i.e., pointwise or
in
, converge to 0 both as a function (i.e., pointwise or
in  ) or as a distribution.
) or as a distribution.
Also, 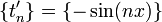 converges to the zero distribution even though
its pointwise limit is not defined.
converges to the zero distribution even though
its pointwise limit is not defined.
Template:Lectures
This article is issued from Wikiversity - version of the Wednesday, June 04, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.