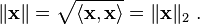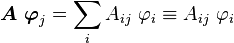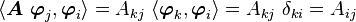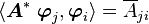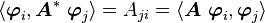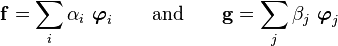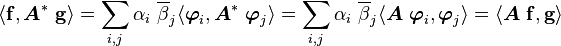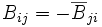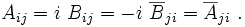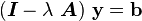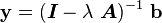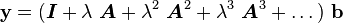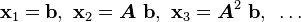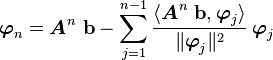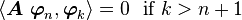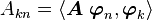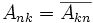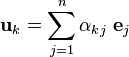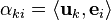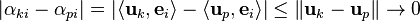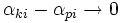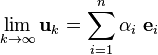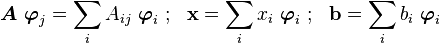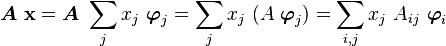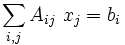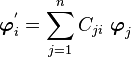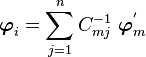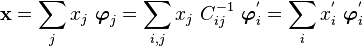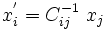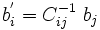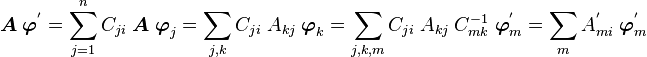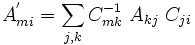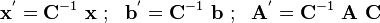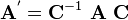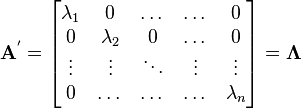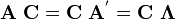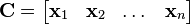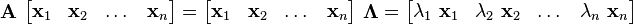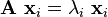Applied linear operators and spectral methods/Lecture 3
< Applied linear operators and spectral methodsReview
In the last lecture we talked about norms in inner product spaces. The induced norm was defined as
We also talked about orthonomal bases and biorthonormal bases. The biorthonormal bases may be thought of as dual bases in the sense that covariant and contravariant vector bases are dual.
The last thing we talked about was the idea of a linear operator. Recall that
where the summation is on the first index.
In this lecture we will learn about adjoint operators, Jacobi tridiagonalization, and a bit about the spectral theory of matrices.
Adjoint operator
Assume that we have a vector space with an orthonormal basis. Then
One specific matrix connected with  is the Hermitian conjugate matrix.
This matrix is defined as
is the Hermitian conjugate matrix.
This matrix is defined as
The linear operator 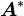 connected with the Hermitian matrix is called the
adjoint operator and is defined as
connected with the Hermitian matrix is called the
adjoint operator and is defined as
Therefore,
and
More generally, if
then
Since the above relation does not involve the basis we see that the adjoint operator is also basis independent.
Self-adjoint/Hermitian matrices
If 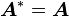 we say that
we say that  is self-adjoint, i.e.,
is self-adjoint, i.e.,
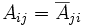 in any orthonomal basis, and the matrix
in any orthonomal basis, and the matrix 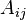 is said to be Hermitian.
is said to be Hermitian.
Anti-Hermitian matrices
A matrix 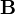 is anti-Hermitian if
is anti-Hermitian if
There is a close connection between Hermitian and anti-Hermitian matrices.
Consider a matrix 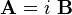 . Then
. Then
Jacobi Tridiagonalization
Let  be self-adjoint and suppose that we want to solve
be self-adjoint and suppose that we want to solve
where 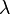 is constant. We expect that
is constant. We expect that
If 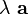 is "sufficiently" small, then
is "sufficiently" small, then
This suggest that the solution should be in the subspace spanned by
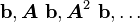 .
.
Let us apply the Gram-Schmidt orthogonalization procedure where
Then we have
This is clearly a linear combination of 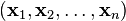 .
Therefore,
.
Therefore, 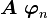 is a linear combination of
is a linear combination of
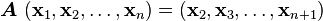 . This
is the same as saying that
. This
is the same as saying that 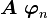 is a linear combination of
is a linear combination of
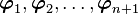 .
.
Therefore,
Now,
But the self-adjointeness of  implies that
implies that
So 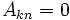 is
is 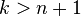 or
or 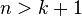 . This is equivalent to expressing
the operator
. This is equivalent to expressing
the operator  as a tridiagonal matrix
as a tridiagonal matrix  which has the form
which has the form
In general, the matrix can be represented in block tridiagonal form.
Another consequence of the Gram-Schmidt orthogonalization is that
Lemma:
Every finite dimensional inner-product space has an orthonormal basis.
Proof:
The proof is trivial. Just use Gram-Schmidt on any basis for that space and
normalize. 
A corollary of this is the following theorem.
Theorem:
Every finite dimensional inner product space is complete.
Recall that a space is complete is the limit of any Cauchy sequence from a subspace of that space must lie within that subspace.
Proof:
Let 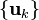 be a Cauchy sequence of elements in the subspace
be a Cauchy sequence of elements in the subspace 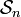 with
with
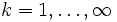 . Also let
. Also let 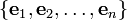 be an
orthonormal basis for the subspace
be an
orthonormal basis for the subspace 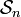 .
.
Then
where
By the Schwarz inequality
Therefore,
But the 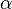 ~s are just numbers. So, for fixed
~s are just numbers. So, for fixed 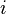 ,
, 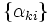 is
a Cauchy sequence in
is
a Cauchy sequence in 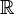 (or
(or 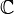 ) and so converges to
a number
) and so converges to
a number 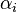 as
as 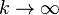 , i.e.,
, i.e.,
which is is the subspace 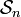 .
. 
Spectral theory for matrices
Suppose 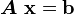 is expressed in coordinates relative to some basis
is expressed in coordinates relative to some basis
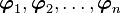 , i.e.,
, i.e.,
Then
So 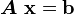 implies that
implies that
Now let us try to see the effect of a change to basis to a new basis
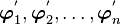 with
with
For the new basis to be linearly independent, 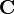 should be invertible so
that
should be invertible so
that
Now,
Hence
Similarly,
Therefore
So we have
In matrix form,
where the objects here are not operators or vectors but rather the matrices and vectors representing them. They are therefore basis dependent.
In other words, the matrix equation 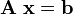
Similarity transformation
The transformation
is called a similarity transformation. Two matrices are equivalent or similar is there is a similarity transformation between them.
Diagonalizing a matrix
Suppose we want to find a similarity transformation which makes  diagonal,
i.e.,
diagonal,
i.e.,
Then,
Let us write 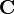 (which is a
(which is a 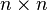 matrix) in terms of its columns
matrix) in terms of its columns
Then,
i.e.,
The pair 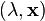 is said to be an eigenvalue pair if
is said to be an eigenvalue pair if 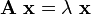 where
where 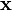 is an eigenvector and
is an eigenvector and 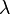 is an eigenvalue.
is an eigenvalue.
Since 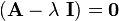 this means that
this means that 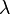 is an
eigenvalue if and only if
is an
eigenvalue if and only if
The quantity on the left hand side is called the characteristic polynomial
and has  roots (counting multiplicities).
roots (counting multiplicities).
In 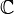 there is always one root. For that root
there is always one root. For that root 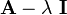 is singular, i.e., there always exists at least one eigenvector.
is singular, i.e., there always exists at least one eigenvector.
We will delve a bit more into the spectral theory of matrices in the next lecture.
| | Resource type: this resource contains a lecture or lecture notes. |
| | Action required: please create Category:Applied linear operators and spectral methods/Lectures and add it to Category:Lectures. |