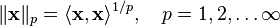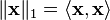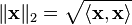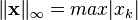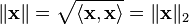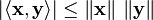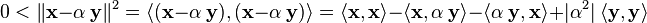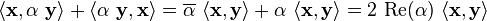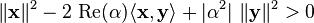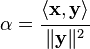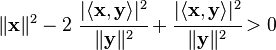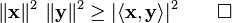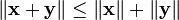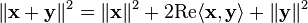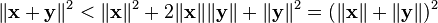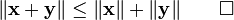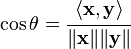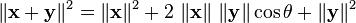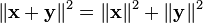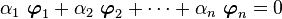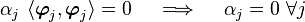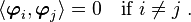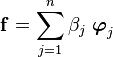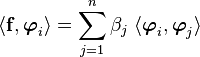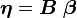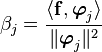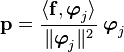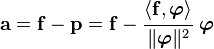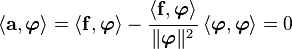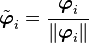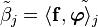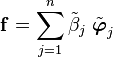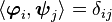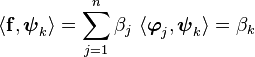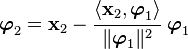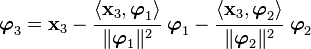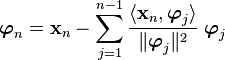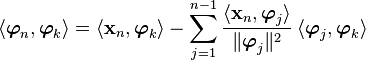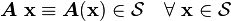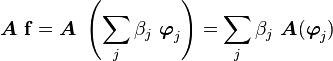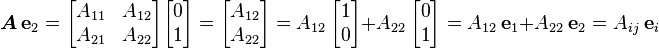Applied linear operators and spectral methods/Lecture 2
< Applied linear operators and spectral methodsNorms in inner product spaces
Inner product spaces have 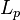 norms which are defined as
norms which are defined as
When 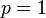 , we get the
, we get the 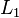 norm
norm
When 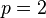 , we get the
, we get the 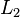 norm
norm
In the limit as 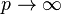 we get the
we get the 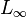 norm or the sup norm
norm or the sup norm
The adjacent figure shows a geometric interpretation of the three norms.
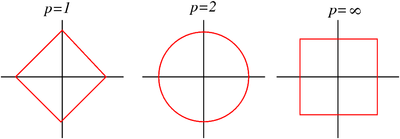 Geomtric interpretation of various norms |
If a vector space has an inner product then the norm
is called the induced norm. Clearly, the induced norm is nonnegative and zero only
if 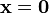 . It is also linear under multiplication by a positive vector. You can
think of the induced norm as a measure of length for the vector space.
. It is also linear under multiplication by a positive vector. You can
think of the induced norm as a measure of length for the vector space.
So useful results that follow from the definition of the norm are discussed below.
Schwarz inequality
In an inner product space
Proof
This statement is true if 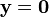 .
.
If 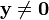 we have
we have
Now
Therefore,
Let us choose 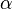 such that it minimizes the left hand side above. This value is
clearly
such that it minimizes the left hand side above. This value is
clearly
which gives us
Therefore,
Triangle inequality
The triangle inequality states that
Proof
From the Schwarz inequality
Hence
Angle between two vectors
In 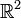 or
or 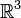 we have
we have
So it makes sense to define 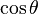 in this way for any real vector space.
in this way for any real vector space.
We then have
Orthogonality
In particular, if 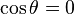 we have an analog of the Pythagoras theorem.
we have an analog of the Pythagoras theorem.
In that case the vectors are said to be orthogonal.
If 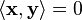 then the vectors are said to be orthogonal even in a complex
vector space.
then the vectors are said to be orthogonal even in a complex
vector space.
Orthogonal vectors have a lot of nice properties.
Linear independence of orthogonal vectors
- A set of nonzero orthogonal vectors is linearly independent.
If the vectors 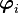 are linearly dependent
are linearly dependent
and the 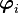 are orthogonal, then taking an inner product with
are orthogonal, then taking an inner product with 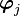 gives
gives
since
Therefore the only nontrivial case is that the vectors are linearly independent.
Expressing a vector in terms of an orthogonal basis
If we have a basis 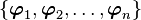 and wish to express a
vector
and wish to express a
vector 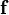 in terms of it we have
in terms of it we have
The problem is to find the 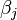 s.
s.
If we take the inner product with respect to 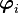 , we get
, we get
In matrix form,
where 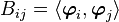 and
and 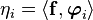 .
.
Generally, getting the 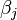 s involves inverting the
s involves inverting the 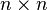 matrix
matrix 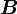 , which is an identity matrix
, which is an identity matrix 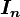 , because
, because 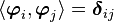 , where
, where 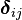 is the Kronecker delta.
is the Kronecker delta.
Provided that the 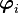 s are orthogonal then we have
s are orthogonal then we have
and the quantity
is called the projection of 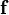 onto
onto 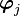 .
.
Therefore the sum
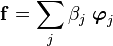
says that 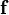 is just a sum of its projections onto the orthogonal basis.
is just a sum of its projections onto the orthogonal basis.
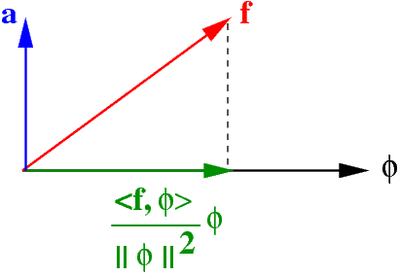 Projection operation. |
Let us check whether 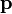 is actually a projection. Let
is actually a projection. Let
Then,
Therefore 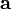 and
and 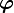 are indeed orthogonal.
are indeed orthogonal.
Note that we can normalize 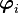 by defining
by defining
Then the basis 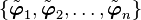 is called an orthonormal basis.
is called an orthonormal basis.
It follows from the equation for 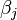 that
that
and
You can think of the vectors 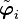 as orthogonal unit vectors in
an
as orthogonal unit vectors in
an 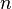 -dimensional space.
-dimensional space.
Biorthogonal basis
However, using an orthogonal basis is not the only way to do things. An alternative that is useful (for instance when using wavelets) is the biorthonormal basis.
The problem in this case is converted into one where, given any basis
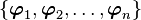 , we want to find another set
of vectors
, we want to find another set
of vectors 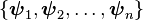 such that
such that
In that case, if
it follows that
So the coefficients 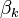 can easily be recovered. You can see a schematic
of the two sets of vectors in the adjacent figure.
can easily be recovered. You can see a schematic
of the two sets of vectors in the adjacent figure.
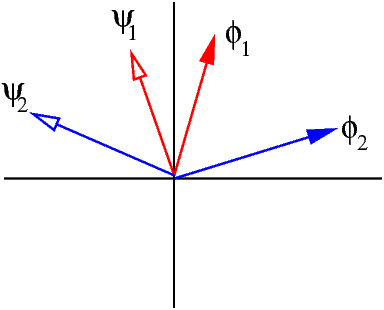 Biorthonomal basis |
Gram-Schmidt orthogonalization
One technique for getting an orthogonal baisis is to use the process of Gram-Schmidt orthogonalization.
The goal is to produce an orthogonal set of vectors
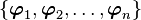 given a linearly independent set
given a linearly independent set
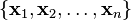 .
.
We start of by assuming that 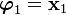 . Then
. Then 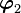 is given by
subtracting the projection of
is given by
subtracting the projection of 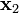 onto
onto 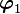 from
from 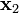 , i.e.,
, i.e.,
Thus 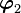 is clearly orthogonal to
is clearly orthogonal to 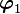 . For
. For 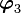 we use
we use
More generally,
If you want an orthonormal set then you can do that by normalizing the orthogonal set of vectors.
We can check that the vectors 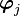 are indeed orthogonal by induction.
Assume that all
are indeed orthogonal by induction.
Assume that all 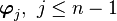 are orthogonal for some
are orthogonal for some 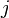 . Pick
. Pick
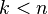 . Then
. Then
Now 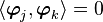 unless
unless 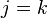 . However, at
. However, at 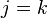 ,
,
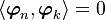 because the two remaining terms cancel out. Hence
the vectors are orthogonal.
because the two remaining terms cancel out. Hence
the vectors are orthogonal.
Note that you have to be careful while numerically computing an orthogonal basis using the Gram-Schmidt technique because the errors add up in the terms under the sum.
Linear operators
The object 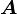 is a linear operator from
is a linear operator from 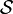 onto
onto 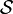 if
if
A linear operator satisfies the properties
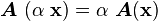 .
.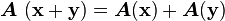 .
.
Note that 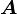 is independent of basis. However, the action of
is independent of basis. However, the action of 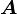 on a basis
on a basis
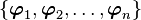 determines
determines 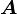 completely since
completely since
Since 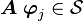 we can write
we can write
where 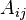 is the
is the 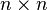 matrix representing the operator
matrix representing the operator 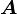 in the basis
in the basis
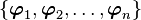 .
.
Note the location of the indices here which is not the same as what we get in matrix
multiplication. For example, in 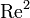 , we have
, we have
We will get into more details in the next lecture.
| | Resource type: this resource contains a lecture or lecture notes. |
| | Action required: please create Category:Applied linear operators and spectral methods/Lectures and add it to Category:Lectures. |