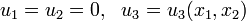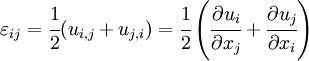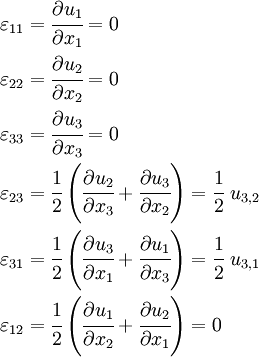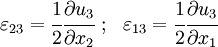Antiplane shear

-- Return to Introduction to Elasticity --

Antiplane shear (or antiplane strain) is the state of strain that is obtained when the displacement field is of the form

u_1 = u_2 = 0, ~~ u_3 = u_3(x_1, x_2)

There is only an out of plane displacement.

Since the strains are given by

\varepsilon_{ij} = \cfrac{1}{2}(u_{i,j} + u_{j,i}) = \cfrac{1}{2}\left(\cfrac{\partial u_i}{\partial x_j} + \cfrac{\partial u_j}{\partial x_i}\right)

we have

\begin{align} \varepsilon_{11} & = \cfrac{\partial u_1}{\partial x_1} = 0 \\ \varepsilon_{22} & = \cfrac{\partial u_2}{\partial x_2} = 0 \\ \varepsilon_{33} & = \cfrac{\partial u_3}{\partial x_3} = 0 \\ \varepsilon_{23} & = \cfrac{1}{2}\left(\cfrac{\partial u_2}{\partial x_3} + \cfrac{\partial u_3}{\partial x_2}\right) = \cfrac{1}{2}~u_{3,2} \\ \varepsilon_{31} & = \cfrac{1}{2}\left(\cfrac{\partial u_3}{\partial x_1} + \cfrac{\partial u_1}{\partial x_3}\right) = \cfrac{1}{2}~u_{3,1} \\ \varepsilon_{12} & = \cfrac{1}{2}\left(\cfrac{\partial u_1}{\partial x_2} + \cfrac{\partial u_2}{\partial x_1}\right) = 0 \end{align}

Therefore, for antiplane shear, the only nonzero strains are the out-of-plane shear strains

\varepsilon_{23} = \cfrac{1}{2}\cfrac{\partial u_3}{\partial x_2} ~;~~ \varepsilon_{13} = \cfrac{1}{2}\cfrac{\partial u_3}{\partial x_1}


This article is issued from Wikiversity - version of the Thursday, August 30, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.