Angular acceleration

Definition

Angular acceleration is a vector whose magnitude is defined as the change in angular velocity in unit time.

It is in 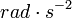$rad\cdot s^{-2}$ in SI unit.

Formula

Analogous to translational acceleration, 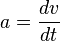$a=\frac{dv}{dt}$ , angular acceleration has the defining formula:

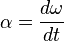
$\alpha=\frac{d\omega}{dt}$

in which 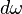$d\omega\,$ represents an instantaneous change in angular velocity,which takes place in 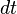$dt\,$ , a short flitting time.

Equivalently, think about the limiting case: 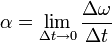$\alpha= \lim_{\Delta t\rightarrow 0}\frac{\Delta\omega}{\Delta t}$

Relationship with Constant Torque

The angular acceleration of an fixed-axis-object is proportional to the net torque applied.

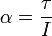
$\alpha=\frac{\tau}{I}$

in which 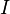$I\,$ is the Moment of Inertia of the object.

Angular Kinematics

When an rotation has constant angular acceleration 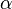$\alpha\,$ , the angle displacement 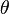$\theta\,$ covered in a given time 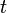$t\,$ is given by an equation that is strikingly similar to the equation for displacement under constant acceleration.

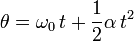
$\theta=\omega_0\,t+\frac{1}{2}\alpha\,t^2$

in which 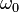$\omega_0\,$ is the angular velocity at the beginning of the time period $t\,$

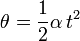
$\theta=\frac{1}{2}\alpha\,t^2$

in which case the angular velocity at the beginning 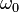$\omega_0\,$ is "zero"

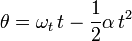
$\theta=\omega_t\,t-\frac{1}{2}\alpha\,t^2$

in which 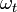$\omega_t\,$ is the angular velocity at the end of the time period $t\,$

This article is issued from Wikiversity - version of the Sunday, April 03, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.