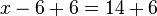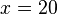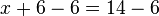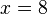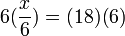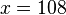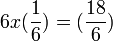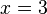Algebraic Properties of Equality

The equal sign that depicts the fact that both sides of it are equal is a very strange symbol with many properties. It tells you various traits of each side, and it allows you to manipulate each side in specific ways. Here are the different properties of that sign:

Property Name	Definition	Example
Reflexive	a = a	7 = 7
Symmetric	If a = b, then b = a	If (3)(2) = 6, then 6 = (3)(2)
Transitive	If a = b & b = c, then a = c	If 8 = (4)(2) and (4)(2) = (2)(4), then 8 = (2)(4)
Substitution	If a = b, then one can replace a with b or vice versa	If a = b and 1 + a = 3, then 1 + b = 3
Addition	You can add one number to both sides of the equation.	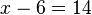$x - 6 = 14\,$ $x - 6 + 6 = 14 + 6\,$ $x=20\,$
Subtraction	You can subtract one number from both sides of the equation.	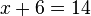$x + 6 = 14\,$ $x + 6 - 6 = 14 - 6\,$ $x = 8\,$
Multiplication	You can multiply both sides of the equation by a number.	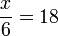$\frac{x}{6} = 18$ $6(\frac{x}{6})= (18)(6)$ $x = 108\,$
Division	You can divide both sides of the equation by a number.	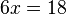$6x = 18\,$ $6x(\frac{1}{6}) = (\frac{18}{6})$ $x = 3\,$

This article is issued from Wikiversity - version of the Wednesday, April 07, 2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.