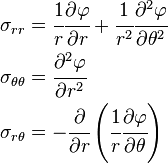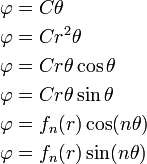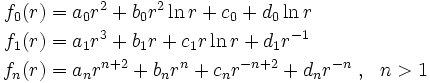Airy stress function
Definition
The Airy stress function (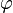 ):
):
- Scalar potential function that can be used to find the stress.
- Satisfies equilibrium in the absence of body forces.
- Only for two-dimensional problems (plane stress/plane strain).
|
If the coordinate basis is rectangular Cartesian Alternatively, if we write the basis as |
|
In polar basis |
|
Something to think about ... Do you think the Airy stress function can be extended to three dimensions? |
Stress equation of compatibility in 2-D
In the absence of body forces,
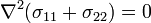
or,
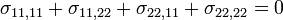
- Note that the stress field is independent of material properties in the absence of body forces (or homogeneous body forces).
- Therefore, the plane strain and plane stress solutions are the same if the boundary conditions are expressed as traction BCS.
In terms of the Airy stress function
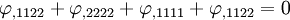
or,
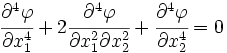
or,
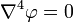
- The stress function
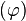 is biharmonic.
is biharmonic. - Any polynomial in
 and
and  of degree less than four is biharmonic.
of degree less than four is biharmonic. - Stress fields that are derived from an Airy stress function which satisfies the biharmonic equation will satisfy equilibrium and correspond to compatible strain fields.
Some biharmonic Airy stress functions
In cylindrical co-ordinates, some biharmonic functions that may be used as Airy stress functions are
where
Displacements in terms of scalar potentials
If the body force is negligible, then the displacements components in 2-D can be expressed as
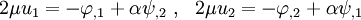
where,
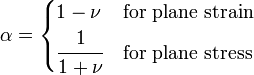
and 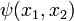 is a scalar displacement potential function that satisfies the conditions
is a scalar displacement potential function that satisfies the conditions
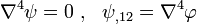
To prove the above, you have to use the plane strain/stress constitutive relations
![\begin{matrix}
\sigma_{\alpha\beta} & = 2\mu\left[\varepsilon_{\alpha\beta} +
\left(\cfrac{1-\alpha}{2\alpha-1}\right)
\varepsilon_{\gamma\gamma}\delta_{\alpha\beta}\right] \\
\varepsilon_{\alpha\beta} & = \cfrac{1}{2\mu}\left[\sigma_{\alpha\beta} +
\left(1-\alpha\right) \sigma_{\gamma\gamma}\delta_{\alpha\beta}\right]
\end{matrix}](../I/m/68608a5c21b36fa695e76eac17cd6fb8.png)
Note also that the plane stress/strain compatibility equations can be written as
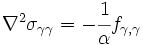
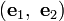 with coordinates denoted by
with coordinates denoted by 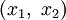 then the Airy stress function
then the Airy stress function 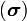 by
by 
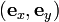 and the coordinates as
and the coordinates as 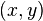 , then the Cauchy stress components are related to the Airy stress function by
, then the Cauchy stress components are related to the Airy stress function by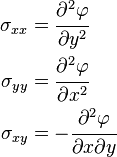
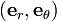 with co-ordinates
with co-ordinates 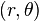 , the Airy stress function is related to the components of the Cauchy stress via
, the Airy stress function is related to the components of the Cauchy stress via