Advanced ANOVA/MANOVA

Resource type: this resource contains a tutorial or tutorial notes. Completion status: this resource is considered to be complete. The purpose of this tutorial is to teach use of multivariate analysis of variance (MANOVA), with practical exercises based on using SPSS. Note that the MANOVA procedure is not available with the Student version of SPSS.

What is MANOVA?

• Developed as a theoretical construct by Samual S. Wilks in 1932 (Biometrika).
• An extension of univariate ANOVA procedures to situations in which there are two or more related dependent variables (ANOVA analyses only a single DV at a time). DVs should be correlated (but not overly so; otherwise they should be combined) or conceptually related.
• The MANOVA procedure identifies (inferentially) whether:
  • Different levels of the IVs have a significant effect on a linear combination of each of the DVs
  • There are interactions between the IVs and a linear combination of the DVs.
  • There are significant univariate effects for each of the DVs separately.

Example

Effects of chemotherapy and memory enhancement training on cognitive functioning in Alzheimer's patients

IVs (factors)

1. Chemotherapy (drug vs no-drug)
2. Memory training (training vs no-training)

DVs

Several measures of cognitive functioning:

1. Test of reading comprehension and retention
2. Memory for names and faces
3. Ratings provided by family members

Usage

• MANOVA is appropriate when we have several DVs which all measure different aspects of some cohesive theme, e.g., several different types of academic achievement (e.g., Maths, English, Science).
• MANOVA works well in situations where there are moderate correlations between DVs. For very high or very low correlation in DVs, it is not suitable: if DVs are too correlated, there isn’t enough variance left over after the first DV is fit, and if DVs are uncorrelated, the multivariate test will lack power (so why sacrifice degrees of freedom?)^[1]
• Alternatively, consider use a series of univariate ANOVAs (one for each DV) or possibly Mixed ANOVA.
• "Because of the increase in complexity and ambiguity of results with MANOVA, one of the best overall recommendations is: Avoid it if you can." (Tabachnick & Fidell, 1983, p.230). In other words - be sure it is really the best approach to use.
• Covariates can also be included → MANCOVA

How does it work?

Simple explanation

• The MANOVA procedure creates a new DV which is a linear combination of the multiple DVs. This particular combination of DVs is chosen to maximise the difference between the IV groups.^[2]
• The MANOVA procedure then assesses whether this new DV differs significantly between the IV groups.^[2]

More complex explanation

MANOVA combines concepts from factorial ANOVA and discriminant analysis:

• It examines the effect of several independent variables (main effects and interaction effects), as does univariate ANOVA
• These IV effects are examined on several DVs that are combined to form one or more linear composites, as in discriminant analysis.
• Factor A main effect - evaluated by combining the original DVs to form one or more orthogonal discriminant functions (roots) which provide the greatest possible separation of the groups representing the levels of Factor A.
• Factor B main effect - evaluated by combining the original DVs to form one or more orthogonal discriminant functions (roots) which provide the greatest possible separation of the groups representing the levels of Factor B.
• A X B Interaction - assessed by forming one or more discriminant functions that maximise the separation of cells of the factorial data matrix.
• For each effect (A, B, and A x B) the discriminant functions will differ (so the composite DV being examined can change)

Assumptions

1. Sample size
   • Rule of thumb: the n in each cell > the number of DVs
   • Larger samples make the procedure more robust to violation of assumptions
2. Normality:
   • MANOVA sig. tests assume multivariate normality, however when cell size > ~20 to 30 the procedure is robust violating this assumption
   • Note that univariate normality is not a guarantee of multivariate normality, but it does help.
   • Check univariate normality via histograms, normal probability plots, skewness, kurtosis, etc. and check multivariate normality using Mahalanobis' distance. These procedures will also help to check for possible outliers.
3. Outliers:
   • MANOVA is sensitive to the effect of outliers (they impact on the Type I error rate); first check for univariate outliers, then use Mahalanobis' distance to check for multivariate outliers (MVOs).
   • MVOs are cases with an unusual combination of scores for the DVs of interest.
   • The SPSS Regression menus can be used to calculate Mahalanobis' Distance, which will provide a score for each case which can be assessed according to a 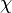² distribution
     • Analyze - Regression - Linear - Dependent (add a unique identifier e.g., ID) - Independent (add all the MANOVA DVs) - Save - MD - Paste/OK.
   • Cases which can be considered MVOs are those with MD values above the critical 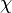² value (where the number of IVs equals is the 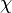² df).
   • MANOVA can tolerate a few outliers, particularly if their scores are not too extreme and there is a reasonable N. If there are too many outliers, or very extreme scores, consider deleting these cases or transforming the variables involved (see Tabachnick & Fidell).
4. Linearity
   • Linear relationships among all pairs of DVs
   • Assess via scatterplots and bivariate correlations (check for each level of the IV(s) i.e., cells - use Split File)
5. Homogeneity of regression
   • This assumption is only important if using stepdown analysis, i.e., there is reason for ordering the DVs.
   • Covariates must have a homogeneity of regression effect (must have equal effects on the DV across the groups)
6. Multicollinearity and singularity
   • MANOVA works best when the DVs are only moderately correlated.
   • When correlations are low, consider running separate ANOVAs
   • When there is strong multicollinearity, there are redundant DVs (singularity) which decreases statistical efficiency.
   • Correlations above .7, and particularly above .8 or .9 are reason for concern.
   • Consider removing one of the strongly correlated pairs or combining them to form a single measure.
7. Homogeneity of variance-covariance matrix (Box's M)
   • The F test from Box’s M statistics should be interpreted cautiously because it is a highly sensitive test of the violation of the multivariate normality assumption, particularly with large sample sizes.
   • MANOVA is fairly robust to this assumption where there are equal sample sizes for each cell.
8. Homogeneity of error variances (Levene's test)
   • If this assumption is violated, use a more conservative critical 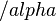level for determining significance for that variable in the univariate F-test. Tabachnick and Fidell suggest .025 or .01 rather than the conventional .05 level.

Multivariate test statistics

Choose from among these multivariate test statistics to assess whether there are statistically significant differences across the levels of the IV(s) for a linear combination of DVs. In general Wilks' 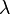is recommended unless there are problems with small N, unequal ns, violations of assumptions, etc. in which case Pillai's trace is more robust^[3]:

Roy's greatest characteristic root

1. Tests for differences on only the first discriminant function
2. Most appropriate when DVs are strongly interrelated on a single dimension
3. Highly sensitive to violation of assumptions - most powerful when all assumptions are met

Wilks' lambda (λ)

1. Most commonly used statistic for overall significance
2. Considers differences over all the characteristic roots
3. The smaller the value of Wilks' lambda, the larger the between-groups dispersion

Hotelling's trace

1. Considers differences over all the characteristic roots

Pillai's criterion

1. Considers differences over all the characteristic roots
2. More robust than Wilks'; should be used when sample size decreases, unequal cell sizes or homogeneity of covariances is violated

Tests of between-subject effects

• What should be done once it is found that an overall F for MANOVA is significant?
• If there is a significant multivariate effect, examine the Tests of Between-Subjects Effects for each of the DVs.
• Since there are multiple tests, control for the Type I error-rate (e.g., use a Bonferroni adjusment - divide the original alpha level by the number of tests).
• However, note that the DVs are usually correlated, therefore this approach would result in confounded results.
• Stepdown F ratios provide a similar approach, without the counfounded results. In this approach, all DVs are prioritised (by the researcher) from most to least important. The most important variable is considered first without correcting for the lower priority variables. All subsequent variables are tested after removing the effects of the higher priority variables (by specifying the higher priority variables as covariates). Thus, stepdown analysis:
  • Is used to assess IV effects on individual DVs
  • Involves computing a univariate F statistic for a DV after eliminating the effects of other DVs preceding it in the analysis.
  • Previous DVs are treated as covariates
  • Somewhat similar to hierarchical multiple linear regression
  • Researcher determines the order in which the DVs are entered, based on some theoretical conceptualisation
  • Is most appropriate when the DVs are correlated.
  • See also: Analyses Following a Significant MANOVA (uwsp.edu)

Effect sizes

Also use effect sizes to evaluate strength of the effects (particularly for significant effects):

• Multivariate ANOVA:
  • Wilks' 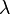- multivariate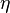 : Wilks' 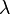reflects the ratio of within-group variance across all discriminant functions to total variance across all discriminant functions.
• Univariate ANOVA:
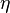  • ² gives the proportion of variance in the DV that is attributable to different levels of an IV.

Pros and cons

Advantages

• Tests the effects of several IVs and several outcome (DVs) within a single analysis.
• Uses the power of convergence (no single operationally defined DV is likely to capture perfectly the conceptual variable of interest)
• IVs of interest are likely to affect a number of different conceptual variables - e.g., an organisation's non-smoking policy may affect employee satisfaction, production, absenteeism, health insurance claims, etc.
• Can provide a more powerful test of significance than available when via univariate tests.
• Reduced Type I error rate compared with performing a series of univariate tests.
• Interpretive advantages over a series of separate univariate ANOVAs.

Disadvantages

• Discriminant functions are not always easy to interpret - they are designed to separate groups, not to make conceptual sense. In MANOVA, each effect evaluated for significance uses different discriminant functions (Factor A may be found to influence a combination of DVs totally different from the combination most affected by Factor B or the interaction between Factors A and B).
• Like discriminant analysis, the assumptions on which it is based are numerous and difficult to assess and meet.

Alternatives

• Combine or eliminate DVs so that only one DV need be analysed.
• Use factor analysis to find orthogonal factors that make up the DVs, then use univariate ANOVAs on each factor (because the factors are orthogonal each univariate analysis should be unrelated)

Example writeup

A one-way multivariate analysis of variance (MANOVA) was conducted to determine the effect of the three types of study strategies (thinking, writing and talking) on two dependent variables (recall and application test scores). A nonsignificant Box’s M, indicated a lack of evidence that the homogeneity of variance-covariance matrix assumption was violated. No univariate or multivariate outliers were evident and MANOVA was considered to be an appropriate analysis technique.

Significant differences were found among the three study strategies on the dependent measures, Wilks’ 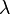= .42, F (4,52) = 7.03, p < .001. The multivariate Wilks' 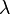was quite strong at .35. Table 1 presents the means and standard deviations of the dependent variables for the three strategies.

Univariate analyses of variance (ANOVAs) for each dependent variable were conducted as follow-up tests to the MANOVA. Using the Bonferroni method for controlling Type I error rates for multiple comparisons, each ANOVA was tested at the .025 level. The ANOVA of the recall scores was significant, F (2,27) = 17.11, p <.001, 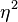= .56, while the ANOVA based on the application scores was nonsignificant, F(2,27)=4.20, p = .026, 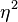=.24.

Post hoc analysis for the recall scores consisted of conducting pairwise comparisons to determine which study strategy affected performance most strongly. Each pairwise comparison was tested at the .025/3, or .008, significance level. The writing group produced significantly superior performance on the recall questions in comparison with either of the other two groups. The thinking and talking groups did not differ significantly from each other.

Table 1 Means and Standard Deviations for each Dependent Variable by Strategy

Note: This table should also include skewness, kurtosis, and descriptives for marginals.

Exercises

Data

• Data: SCHL8.sav (Francis 5.3; p. 132 (5th ed.))

1st MANOVA

• DVs (Academic achievement):
  • Maths (mathsach)
  • English (engach)
• IVs:
  • Socio-economic status (SES; Low, Moderate, High)

2nd MANOVA

• DVs (Classroom behaviour):
  • Attentiveness in Year 8 (attent)
  • Settledness in Year 8 (settle)
  • Sociability in Year 8 (sociab)
• IVs:
  • Gender (Sex; Male, Female)

SPSS Steps

• Analyze - General Linear Model - Multivariate (add IV(s) (fixed factors) and DVs)
• Graphs - could use any of:
  • Clustered Bar Chart (Summaries of separate variables) or
  • Clustered Error-bar (Summaries of separate variables) or
  • Multiple Line Graph (Summaries of separate variables)

3rd MANOVA (within-subjects)

• DVs
  • Year level or Time
    • Year 7 and 8 (same participants over Time)
  • Classroom behaviour
    • Attentiveness
    • Settledness
    • Sociability

4th MANOVA (within-subjects)

• DVs
  • Students' perceptions of maths and english teachers
    • Maths and English teachers (same students assessing these)
  • Student ratings of teacher qualities
    • Responsiveness
    • Expectations
    • Enjoyable class

References

1. ↑ French, A., Poulsen, J., & Yu, A. (2002). Multivariate Analysis of Variance (MANOVA).
2. ↑ 2.0 2.1 Francis, G. (2007). Introduction to SPSS for Windows: v. 15.0 and 14.0 with Notes for Studentware (5th ed.). Sydney: Pearson Education. (Section 5.3)
3. ↑ Tabachnick, B. G., & Fidell, L. S. (1983). Using multivariate statistics. New York: Harper & Row. (Chapter 9; more recent editions are available

• Hair, J. F., Anderson, R. E., Tatham, R. L., & Black, W. C. (1998). Multivariate data analysis (5th ed.). New York: Macmillan (Chapter 6).
• Pallant, J. (2005). SPSS survival manual: A step by step guide to data analysis using SPSS for Windows (Versions 12-14). Crows Nest, NSW, Australia: Allen & Unwin. (Chapter 21)

See also

• MANOVA

External links

• MANOVA (ucspace)
• MANOVA Notes (Handout)