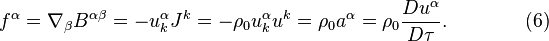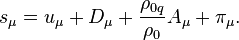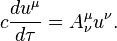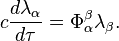Acceleration tensor
The acceleration tensor is an antisymmetric tensor describing the 4-acceleration of particles and consisting of six components. The tensor components are at the same time the components of two three-dimensional vectors – the acceleration field strength and the solenoidal acceleration vector. The acceleration field stress-energy tensor, the acceleration field equations and the four-force density are determined with the help of the acceleration tensor. Acceleration field in matter is a component of general field.
Definition
The expression for the acceleration tensor can be found in papers by Sergey Fedosin, [1] where the tensor is defined using the 4-curl:
Here the acceleration 4-potential 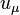 is given by:
is given by:
where 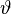 is the scalar potential,
is the scalar potential,
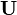 is the vector potential of acceleration field,
is the vector potential of acceleration field,
 is the speed of light.
is the speed of light.
Expression for the components
The acceleration field strength and the solenoidal acceleration vector are found with the help of (1):
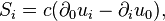
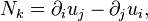 and in the second expression three numbers
and in the second expression three numbers 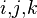 are composed of non-recurring sets 1,2,3; or 2,1,3; or 3,2,1 etc.
are composed of non-recurring sets 1,2,3; or 2,1,3; or 3,2,1 etc.
In vector notation we can write:
The acceleration tensor consists of the components of these vectors:
The transition to the acceleration tensor with contravariant indices is carried out by multiplying by double metric tensor:
In the special relativity, this tensor has the form:
For the vectors, related to the specific point particle, we can write:
where 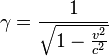 ,
, 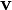 is the velocity of the particle.
is the velocity of the particle.
To transform the components of the acceleration tensor from one inertial system to another we must take into account the transformation rule for tensors. If the reference frame K' moves with an arbitrary constant velocity 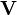 with respect to the fixed reference frame K, and the axes of the coordinate systems are parallel to each other, the acceleration field strength and the solenoidal acceleration vector are transformed as follows:
with respect to the fixed reference frame K, and the axes of the coordinate systems are parallel to each other, the acceleration field strength and the solenoidal acceleration vector are transformed as follows:
Properties of the tensor
-
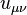 is an antisymmetric tensor of rank 2, from this the condition follows:
is an antisymmetric tensor of rank 2, from this the condition follows: 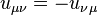 . Three of the six independent components of the acceleration tensor are associated with the components of the acceleration field strength
. Three of the six independent components of the acceleration tensor are associated with the components of the acceleration field strength 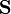 , and the other three – with the components of the solenoidal acceleration vector
, and the other three – with the components of the solenoidal acceleration vector 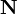 . Due to antisymmetry such an invariant as the contraction of the tensor with the metric tensor vanishes:
. Due to antisymmetry such an invariant as the contraction of the tensor with the metric tensor vanishes: 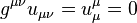 .
. - Contraction of the tensor with itself
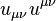 is an invariant, and contraction of the tensor product with Levi-Civita symbol as
is an invariant, and contraction of the tensor product with Levi-Civita symbol as 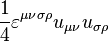 is a pseudoscalar invariant. These invariants in the special theory of relativity can be expressed as follows:
is a pseudoscalar invariant. These invariants in the special theory of relativity can be expressed as follows:
- Determinant of the tensor is also a Lorentz invariant:
Acceleration field
The acceleration field equations are written with the acceleration tensor:
where 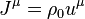 is the mass 4-current,
is the mass 4-current, 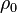 is the mass density in the comoving reference frame,
is the mass density in the comoving reference frame, 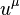 is the 4-velocity,
is the 4-velocity, 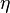 is a constant determined in each task.
is a constant determined in each task.
Instead of (2) it is possible to use the expression:
Equation (2) is satisfied identically, which is proved by substituting into it the definition for the acceleration tensor according to (1). If in (2) we insert the tensor components 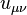 , this leads to two vector equations:
, this leads to two vector equations:
According to (5), the solenoidal acceleration vector has no sources since its divergence vanishes. From (4) it follows that the time variation of the solenoidal acceleration vector leads to emerging of the curl of the acceleration field strength.
Equation (3) relates the acceleration field to its source in the form of the mass 4-current. In Minkowski space of the special theory of relativity the equation form is simplified and becomes:
where 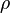 is the density of moving mass,
is the density of moving mass,
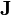 is the density of mass current.
is the density of mass current.
According to the first of these equations, the acceleration field strength is generated by the mass density, and according to the second equation the mass current or the change in time of the acceleration field strength generate the circular field of the solenoidal acceleration vector.
From (3) and (1) can be obtained continuity equation:
This equation means that thanks to the curvature of space-time when the Ricci tensor 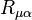 is non-zero, the acceleration tensor
is non-zero, the acceleration tensor 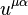 is a possible source of divergence of mass 4-current. If space-time is flat, as in Minkowski space, the left side of the equation is set to zero, the covariant derivative becomes the 4-gradient and remains the following:
is a possible source of divergence of mass 4-current. If space-time is flat, as in Minkowski space, the left side of the equation is set to zero, the covariant derivative becomes the 4-gradient and remains the following:
Covariant theory of gravitation
Action and Lagrangian
The total Lagrangian for the substance in the gravitational and electromagnetic fields includes the acceleration tensor and is part of the action function: [1]
where 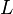 is the Lagrangian,
is the Lagrangian, 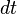 is the differential of the coordinate time,
is the differential of the coordinate time, 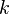 is a certain coefficient,
is a certain coefficient, 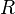 is the scalar curvature,
is the scalar curvature, 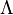 is the cosmological constant, which is a function of the system,
is the cosmological constant, which is a function of the system,  is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions,
is the speed of light as a measure of the propagation speed of electromagnetic and gravitational interactions, 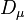 is the gravitational four-potential,
is the gravitational four-potential, 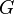 is the gravitational constant,
is the gravitational constant, 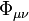 is the gravitational tensor,
is the gravitational tensor, 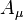 is the electromagnetic 4-potential,
is the electromagnetic 4-potential, 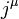 is the electromagnetic 4-current,
is the electromagnetic 4-current, 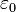 is the vacuum permittivity,
is the vacuum permittivity, 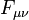 is the electromagnetic tensor,
is the electromagnetic tensor, 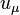 is the 4-potential of acceleration field,
is the 4-potential of acceleration field, 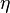 and
and 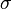 are some constants,
are some constants, 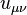 is the acceleration tensor,
is the acceleration tensor, 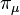 is the 4-potential of the pressure field,
is the 4-potential of the pressure field, 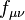 is the pressure field tensor,
is the pressure field tensor, 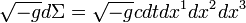 is the invariant 4-volume,
is the invariant 4-volume, 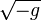 is the square root of the determinant
is the square root of the determinant 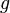 of the metric tensor, taken with a negative sign,
of the metric tensor, taken with a negative sign, 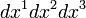 is the product of differentials of the spatial coordinates.
is the product of differentials of the spatial coordinates.
The variation of the action function by 4-coordinates leads to the equation of motion of the substance unit in the gravitational and electromagnetic fields and the pressure field:
where 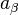 is the 4-acceleration with the covariant index, the operator of proper-time-derivative with respect to the proper time
is the 4-acceleration with the covariant index, the operator of proper-time-derivative with respect to the proper time 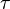 is used, the first term on the right is the gravitational force density, expressed with the help of the gravitational field tensor, the second term is the Lorentz electromagnetic force density for the charge density
is used, the first term on the right is the gravitational force density, expressed with the help of the gravitational field tensor, the second term is the Lorentz electromagnetic force density for the charge density 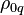 measured in the comoving reference frame, and the last term sets the pressure force density, and the relation holds:
measured in the comoving reference frame, and the last term sets the pressure force density, and the relation holds:
In the special theory of relativity, this relation is simplified and can be written in the form of two expressions:
where 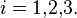
If we vary the action function by the acceleration 4-potential, we obtain the acceleration field equation (3).
Acceleration field stress-energy tensor
With the help of the acceleration tensor in the covariant theory of gravitation the acceleration stress-energy tensor is constructed:
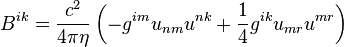 .
.
The covariant derivative of the acceleration field stress-energy tensor determines the four-force density:
Generalized velocity and Hamiltonian
The covariant 4-vector of generalized velocity is given by:
With regard to the generalized 4-velocity, the Hamiltonian contains the acceleration tensor and has the form:
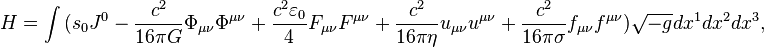
where 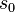 and
and 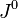 are the time components of the 4-vectors
are the time components of the 4-vectors 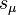 and
and 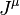 .
.
In the reference frame that is fixed relative to the system's center of mass, the Hamiltonian will determine the invariant energy of the system.
Special theory of relativity
Studying Lorentz covariance of the 4-force, Friedman and Scarr found incomplete covariance of the expression for the 4-force in the form 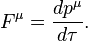 [2]
[2]
This led them to conclude that the 4-acceleration must be expressed with the help of some antisymmetric tensor 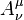 :
:
Based on the analysis of different types of motion, they estimated the required values of the components of the acceleration tensor, thereby giving this tensor indirect definition.
From comparison with (6) it follows that the tensor 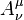 coincides with the acceleration tensor
coincides with the acceleration tensor 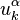 up to a sign and a constant factor.
up to a sign and a constant factor.
Mashhoon and Muench considered transformation of inertial reference frames, associated with the accelerated reference frame, and came to the relation: [3]
The tensor 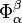 has the same properties as the acceleration tensor
has the same properties as the acceleration tensor 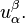
Other theories
In the articles [4] [5] [6]
devoted to the modified Newtonian dynamics (MOND), in the tensor-vector-scalar gravity appear scalar function 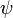 or
or 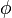 , that defines a scalar field, and 4-vector
, that defines a scalar field, and 4-vector 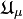 or
or 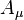 , and 4-tensor
, and 4-tensor ![\mathfrak {U}_{[\mu\nu ]}](../I/m/4f9a22c82a2956b92d7f39834617cf8c.png) or
or 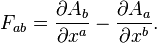
The analysis of these values in the corresponding Lagrangian demonstrates that scalar function 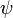 or
or 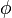 correspond to scalar potential
correspond to scalar potential 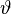 of the acceleration field; 4-vector
of the acceleration field; 4-vector 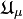 or
or 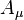 correspond to 4-potential
correspond to 4-potential 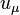 of the acceleration field; 4-tensor
of the acceleration field; 4-tensor ![\mathfrak {U}_{[\mu\nu ]}](../I/m/4f9a22c82a2956b92d7f39834617cf8c.png) or
or 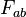 correspond to acceleration tensor
correspond to acceleration tensor 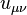 .
.
As it is known, the acceleration field is not intended to explain the accelerated motion, but for its accurate description. In this case, it can be assumed that the tensor-vector-scalar theories cannot pretend to explain the rotation curves of galaxies. At best, they can only serve to describe the motion, for example to describe the rotation of stars in galaxies and the rotation of galaxies in clusters of galaxies.
See also
- Acceleration field
- Electromagnetic tensor
- Gravitational tensor
- Pressure field tensor
- Dissipation field tensor
- Acceleration stress-energy tensor
- General field
- Dissipation field
- Pressure field
- Lorentz-invariant theory of gravitation
- Covariant theory of gravitation
References
- 1 2 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014.
- ↑ Yaakov Friedman and Tzvi Scarr. Covariant Uniform Acceleration. Journal of Physics: Conference Series Vol. 437 (2013) 012009 doi:10.1088/1742-6596/437/1/012009.
- ↑ Bahram Mashhoon and Uwe Muench. Length measurement in accelerated systems. Annalen der Physik. Vol. 11, Issue 7, P. 532–547, 2002.
- ↑ J. D. Bekenstein and M. Milgrom, Does the Missing Mass Problem Signal the Breakdown of Newtonian Gravity ? Astrophys. Journ. 286, 7 (1984).
- ↑ Bekenstein, J. D. (2004), Relativistic gravitation theory for the modified Newtonian dynamics paradigm, Physical Review D 70 (8): 083509, https://dx.doi.org/10.1103%2FPhysRevD.70.083509 .
- ↑ Exirifard, Q. (2013), GravitoMagnetic Field in Tensor-Vector-Scalar Theory, Journal of Cosmology and Astroparticle Physics, JCAP04: 034, https://dx.doi.org/10.1088%2F1475-7516%2F2013%2F04%2F034.
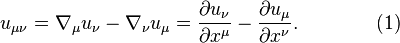
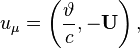
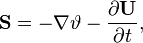

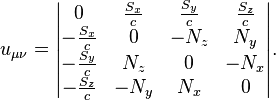
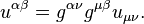
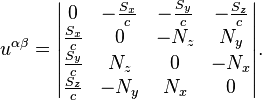
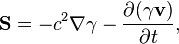
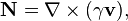
![\mathbf {S}^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {S}) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {S}-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {S}) + [\mathbf {V} \times \mathbf {N }] \right),](../I/m/946e5199297eb3bb8f55044bd730a98c.png)
![\mathbf {N }^\prime = \frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {N }) + \frac {1}{\sqrt{1 - {V^2 \over c^2}}} \left(\mathbf {N }-\frac {\mathbf {V}}{V^2} (\mathbf {V}\cdot \mathbf {N }) - \frac {1}{ c^2} [\mathbf {V} \times \mathbf {S}] \right).](../I/m/59e34295dc9d0431343658672d1dd9e5.png)
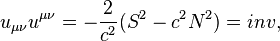
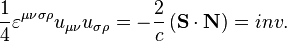
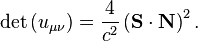
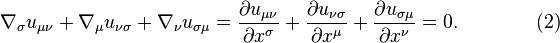
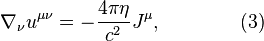
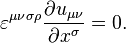
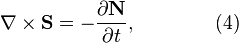

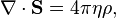
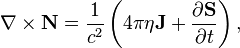
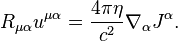
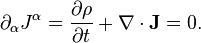
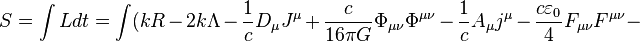
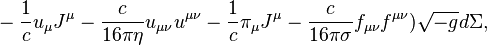
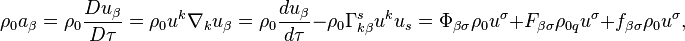
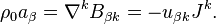
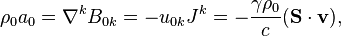
![~ \rho_0 a_i = \nabla^k B_{i k} = - u_{i k} J^k = \gamma \rho_0 (\mathbf{S }+ [\mathbf {v} \times \mathbf {N}] ),](../I/m/48f3c83725c7345b55e43e7ea8c7e2c3.png)