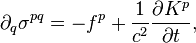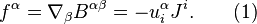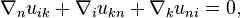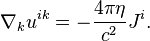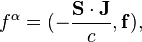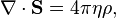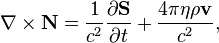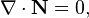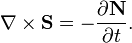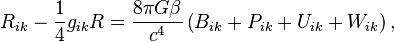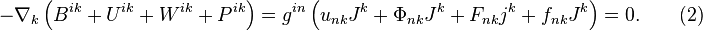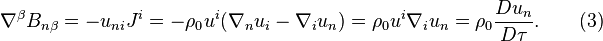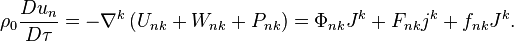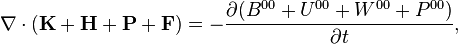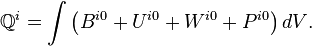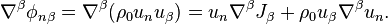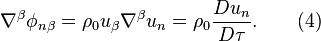Acceleration stress-energy tensor
Acceleration field stress-energy tensor is a symmetric four-dimensional tensor of the second valence (rank), which describes the density and flux of energy and momentum of the acceleration field in the substance. This tensor as well as the gravitational stress-energy tensor, the pressure stress-energy tensor, the dissipation stress-energy tensor and the stress-energy tensor of the electromagnetic field are included in the equation for determining the metric in the covariant theory of gravitation. The covariant derivative of the acceleration field stress-energy tensor allows us to determine the density of the acceleration force acting in the substance.
Covariant theory of gravitation
Definition
In the covariant theory of gravitation (CTG) the acceleration field is considered not a scalar field but a 4-vector field consisting of scalar and 3-vector components. In CTG the acceleration field stress-energy tensor was defined by Fedosin with the help of the acceleration tensor 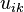 and the metric tensor
and the metric tensor 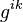 based on the principle of least action: [1]
based on the principle of least action: [1]
where 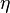 is a constant defined in terms of the fundamental constants and physical parameters of the system. Acceleration field is considered as a component of the general field.
is a constant defined in terms of the fundamental constants and physical parameters of the system. Acceleration field is considered as a component of the general field.
Components of the acceleration stress-energy tensor
Since the acceleration tensor consists of the components of the acceleration field strength 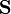 and the solenoidal acceleration vector
and the solenoidal acceleration vector 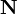 , then the acceleration field stress-energy tensor can be expressed using these components. In the limit of the special theory of relativity the metric tensor does not depend on the coordinates and time, and in this case the acceleration field stress-energy tensor acquires the simplest form:
, then the acceleration field stress-energy tensor can be expressed using these components. In the limit of the special theory of relativity the metric tensor does not depend on the coordinates and time, and in this case the acceleration field stress-energy tensor acquires the simplest form:
The time components of the tensor denote:
1) The volumetric energy density of the acceleration field
2) The vector of the momentum density of the acceleration field 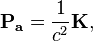 where the vector of the energy flux density of the acceleration field is
where the vector of the energy flux density of the acceleration field is
Due to the symmetry of the tensor indices,  , hence
, hence 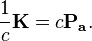
3) The space components of the tensor form a submatrix 3 x 3, which is the 3-dimensional tensor of the momentum flux density of the acceleration field, taken with a minus sign. The 3-dimensional tensor can be written as follows:
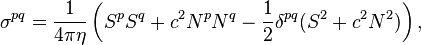
where 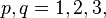 the components
the components 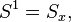
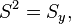


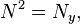
 the Kronecker delta
the Kronecker delta 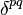 equals 1 if
equals 1 if 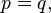 and equals 0 if
and equals 0 if 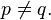
Three-dimensional divergence of the tensor of the momentum flux density of the acceleration field relates the force density and the rate of change of the momentum density of the acceleration field:
where 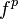 denote the components of the three-dimensional acceleration force density,
denote the components of the three-dimensional acceleration force density, 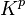 are the components of the energy flux density of the acceleration field.
are the components of the energy flux density of the acceleration field.
4-force density and field equations
The principle of least action implies that the 4-vector of force density 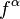 can be found with the help of either the acceleration field stress-energy tensor, or the product of the acceleration field tensor and the mass 4-current:
can be found with the help of either the acceleration field stress-energy tensor, or the product of the acceleration field tensor and the mass 4-current:
The acceleration field equations can be written as follows:
In the special theory of relativity, according to (1) we can write for the components of the four-force density the following:
where ![~ \mathbf{f}= - \rho \mathbf{S} - [\mathbf{J} \times \mathbf{N} ]](../I/m/f6b7e5471a05d8eaecac832dbb14d5f6.png) is the 3-vector of the force density,
is the 3-vector of the force density, 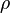 is the density of the moving substance,
is the density of the moving substance, 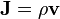 is the 3-vector of the mass current density,
is the 3-vector of the mass current density, 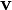 is the 3-vector of the velocity of the substance unit.
is the 3-vector of the velocity of the substance unit.
In Minkowski space, the field equations are transformed into 4 equations for the acceleration field strength 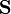 and the solenoidal acceleration vector
and the solenoidal acceleration vector 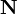
Equation for the metric
In the covariant theory of gravitation the acceleration field stress-energy tensor in accordance with the principles of metric theory of relativity is one of the tensors defining the metric inside the bodies by means of the equation for the metric:
where 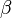 is the coefficient to be determined,
is the coefficient to be determined, 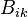 ,
, 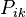 ,
, 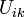 and
and 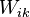 are the stress-energy tensors of the acceleration field, pressure field, gravitational and electromagnetic fields, respectively,
are the stress-energy tensors of the acceleration field, pressure field, gravitational and electromagnetic fields, respectively, 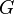 is the gravitational constant.
is the gravitational constant.
Equation of motion
The equation of motion of a point particle inside or outside the substance can be represented in the tensor form, using the acceleration field stress-energy tensor 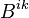 or acceleration tensor
or acceleration tensor 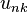 :
:
where 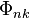 is the gravitational field tensor ,
is the gravitational field tensor , 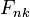 is the electromagnetic tensor,
is the electromagnetic tensor, 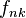 is the pressure field tensor,
is the pressure field tensor,
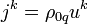 is the charge 4-current,
is the charge 4-current, 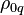 is the density of the electric charge of the substance unit in the reference frame at rest,
is the density of the electric charge of the substance unit in the reference frame at rest, 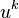 is the 4-velocity.
is the 4-velocity.
Now we should take into account that 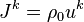 is the mass 4-current, and the acceleration tensor is determined through the covariant 4-velocity in the form
is the mass 4-current, and the acceleration tensor is determined through the covariant 4-velocity in the form 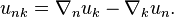 This gives the following:
This gives the following:
Here operator of proper-time-derivative 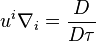 is used, where
is used, where 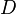 is the symbol of 4-differential in the curved spacetime,
is the symbol of 4-differential in the curved spacetime, 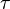 is the proper time,
is the proper time, 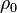 is the mass density in the comoving frame.
is the mass density in the comoving frame.
Accordingly, the equation of motion (2) has the form:
The time component of this equation at 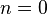 describes the change in the energy, and the space component at
describes the change in the energy, and the space component at 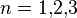 relates the acceleration with the force density.
relates the acceleration with the force density.
Conservation laws
When the index 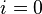 in (2), i.e. for the time component of the equation, in the limit of the special theory of relativity from the vanishing of the left side of (2) it follows:
in (2), i.e. for the time component of the equation, in the limit of the special theory of relativity from the vanishing of the left side of (2) it follows:
where 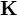 is the vector of the acceleration field energy flux density,
is the vector of the acceleration field energy flux density, 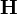 is the Heaviside vector,
is the Heaviside vector, 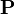 is the Poynting vector,
is the Poynting vector, 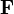 is the vector of the pressure field energy flux density.
is the vector of the pressure field energy flux density.
This equation can be regarded as the local conservation law of energy-momentum of the four fields.
The integral form of the law of conservation of energy-momentum is obtained by integrating (2) over the 4-volume. In integration of (2) the Gauss's formula is used, according to which integration of divergence of the tensor sum over the 4-volume is substituted with integration of the sum of the tensor time components over the 3-volume. As a result, in Lorentz coordinates the conserved 4-vector equal to zero is obtained: [2]
Vanishing of the 4-vector allows us to explain the 4/3 problem, according to which the mass-energy of the field in the field momentum of a moving system is 4/3 times greater than in the field energy of a fixed system.
Relativistic mechanics
As in relativistic mechanics, so in general theory of relativity (GTR), the acceleration field stress-energy tensor is not used. Instead of it the so-called stress-energy tensor of matter is used, which in the simplest case has the following form: 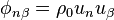 . In GTR, the tensor
. In GTR, the tensor 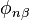 is substituted into the equation for the metric and its covariant derivative gives the following:
is substituted into the equation for the metric and its covariant derivative gives the following:
In GTR it is assumed that the continuity equation holds in the form 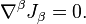 Then, using the operator of the proper time derivative the covariant derivative of the tensor
Then, using the operator of the proper time derivative the covariant derivative of the tensor 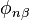 gives the product of the density and 4-acceleration, i.e. the density of 4-force:
gives the product of the density and 4-acceleration, i.e. the density of 4-force:
However, the continuity equation is valid only in the special theory of relativity in the form 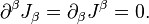 In curved spacetime, instead of it the equation
In curved spacetime, instead of it the equation 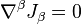 should be used, but in the right side of this equation instead of zero an additional non-zero term with Riemann curvature tensor appears. [1] Consequently, (4 ) is not an exact expression, and the tensor
should be used, but in the right side of this equation instead of zero an additional non-zero term with Riemann curvature tensor appears. [1] Consequently, (4 ) is not an exact expression, and the tensor 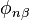 determines the substance properties only in the special theory of relativity. In contrast, in the covariant theory of gravitation, equation (3) is written in a covariant form, so that the acceleration field stress-energy tensor
determines the substance properties only in the special theory of relativity. In contrast, in the covariant theory of gravitation, equation (3) is written in a covariant form, so that the acceleration field stress-energy tensor 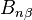 describes the acceleration field of the substance particles in the curved Riemannian spacetime as well.
describes the acceleration field of the substance particles in the curved Riemannian spacetime as well.
See also
- Acceleration field
- Gravitational stress-energy tensor
- Pressure stress-energy tensor
- Dissipation stress-energy tensor
- Electromagnetic stress-energy tensor
- Acceleration tensor
- General field
- Dissipation field
- Pressure field
References
- 1 2 Fedosin S.G. About the cosmological constant, acceleration field, pressure field and energy. vixra.org, 5 Mar 2014.
- ↑ Fedosin S.G. The Integral Energy-Momentum 4-Vector and Analysis of 4/3 Problem Based on the Pressure Field and Acceleration Field. American Journal of Modern Physics. Vol. 3, No. 4, 2014, pp. 152-167. doi: 10.11648/j.ajmp.20140304.12.
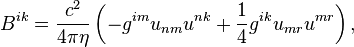
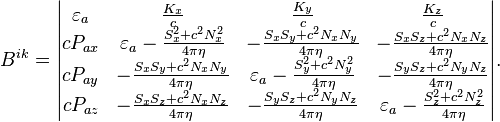
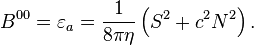
![~\mathbf{K} = \frac{ c^2 }{4 \pi \eta }[\mathbf{S}\times \mathbf{N}].](../I/m/c0522879794118a736fd3d086ee1c405.png)